Question

【题目】如图，已知⊙O为△ABC的外接圆，圆心O在这个三角形的高CD上，E，F分别是边AC和BC上的中点，试判断四边形CEDF的形状，并加以说明．

Answer 1

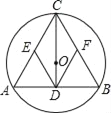
【答案】四边形CEDF为菱形．证明见解析.

【解析】

由垂径定理知，点D是AB的中点，有AD＝BD，可证△CAD≌△CBD，可得AC＝BC；由E，F分别为AC，BC的中点，D为AB中点，得DF＝CE＝AC，DE＝CF＝BC，即DE＝DF＝CE＝CF，从而可得四边形CEDF为菱形．

四边形CEDF为菱形．

证明：∵AB为弦，CD为直径所在的直线且AB⊥CD，

∴AD＝BD，∠ADC＝∠CDB，

在△ADC和△BDC中

，

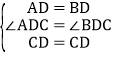∴△CAD≌△CBD（SAS），

∴AC＝BC；

又∵E，F分别为AC，BC的中点，D为AB中点，

∴DF＝CE＝AC，DE＝CF＝BC，

∴DE＝DF＝CE＝CF，

∴四边形CEDF为菱形．