题目内容
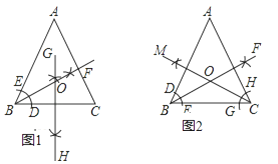
【题目】如图所示,直线AB和CD与直线MN相交.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足________时,AB∥CD;
(2)如图②,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足________时,AB∥CD;
(3)如图③,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD?请说明理由.

【答案】(1)∠1+∠2=90°;(2)∠1=∠2;(3)∠1=∠2,理由详见解析.
【解析】
(1)根据角平分线定义得出∠BEF=2∠1,∠DFE=2∠2,∠1+∠2=90°时,求出∠BEF+∠DFE=180°,根据平行线的判定推出即可.
(2)根据角平分线定义得出∠BEM=2∠1,∠DFE=2∠2,求出∠BEM=∠DFE,根据平行线的判定推出即可.
(3)根据角平分线定义得出∠AEF=2∠1,∠DFE=2∠2,求出∠AEF=∠DFE,根据平行线的判定推出即可.
解:(1)∠1+∠2=90°时,AB∥CD,
理由是:EG平分∠BEF,FH平分∠DFE,
∴∠BEF=2∠1,∠DFE=2∠2,
∵∠1+∠2=90°,
∴∠BEF+∠DFE=180°,
∴AB∥CD,
故答案为:∠1+∠2=90°.
(2)∠1=∠2,
理由是:EG平分∠BEM,FH平分∠DFE,
∴∠BEM=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠BEM=∠DFE,
∴AB∥CD,
故答案为:∠1=∠2.
(3)∠1=∠2,
理由是:EG平分∠AEF,FH平分∠DFE,
∴∠AEF=2∠1,∠DFE=2∠2,
∵∠1=∠2,
∴∠AEF=∠DFE,
∴AB∥CD.

【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.