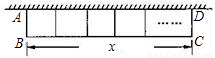
题目内容
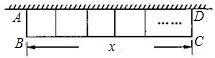
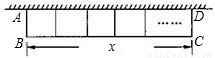
如图,一面利用墙,用篱笆围成一个外形为矩形的花圃,花圃的面积为S平方米,平行于院墙的一边长为x米.
(1)若院墙可利用最大长度为10米,篱笆长为24米,花圃中间用一道篱笆间隔成两个小矩形,求S与x之间函数关系.
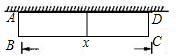
(2)在(1)的条件下,围成的花圃面积为45平方米时,求AB的长.能否围成面积比45平方米更大的花圃?如果能,应该怎么围?如果不能请说明理由.
(3)当院墙可利用最大长度为40米,篱笆长为77米,中间建n道篱笆间隔成小矩形,当这些小矩形为正方形,且x为正整数时,请直接写出一组满足条件的x,n的值.
解:(1)由题意得:
S=x×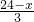 =
= x2+8x (0<x≤10)
x2+8x (0<x≤10)
(2)由S= x2+8x=45,
x2+8x=45,
解得;x1=15(舍去),x2=9,
∴x=9,AB=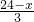 =5,
=5,
又S= x2+8x=
x2+8x= (x-12)2+48,0<x≤10,
(x-12)2+48,0<x≤10,
∵当x≤10时,S随x的增大而增大,
∴当x=10米时,S最大,为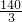 平方米>45平方米,
平方米>45平方米,
∴平行于院墙的一边长为10时,就能围成面积比45平方米更大的花圃.
(3)根据题意可得: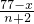 =
=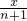 ,
,
n=4;x=35
分析:(1)根据等量关系“花圃的面积=花圃的长×花圃的宽”列出函数关系式,并确定自变量的取值范围;
(2)令S=45,将其代入所求得的函数关系式里求得x,再算出AB的长.通过函数关系式求得S的最大值,得出能否围成面积比45平方米更大的花圃;
(3)根据等量关系“花圃的长=(n+1)×花圃的宽”写出符合题中条件的x,n.
点评:本题考查了同学们列函数关系式并求解最值的能力,同时需要注意自变量的取值范围.
S=x×
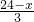 =
= x2+8x (0<x≤10)
x2+8x (0<x≤10)(2)由S=
 x2+8x=45,
x2+8x=45,解得;x1=15(舍去),x2=9,
∴x=9,AB=
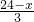 =5,
=5,又S=
 x2+8x=
x2+8x= (x-12)2+48,0<x≤10,
(x-12)2+48,0<x≤10,∵当x≤10时,S随x的增大而增大,
∴当x=10米时,S最大,为
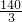 平方米>45平方米,
平方米>45平方米,∴平行于院墙的一边长为10时,就能围成面积比45平方米更大的花圃.
(3)根据题意可得:
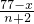 =
=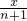 ,
,n=4;x=35
分析:(1)根据等量关系“花圃的面积=花圃的长×花圃的宽”列出函数关系式,并确定自变量的取值范围;
(2)令S=45,将其代入所求得的函数关系式里求得x,再算出AB的长.通过函数关系式求得S的最大值,得出能否围成面积比45平方米更大的花圃;
(3)根据等量关系“花圃的长=(n+1)×花圃的宽”写出符合题中条件的x,n.
点评:本题考查了同学们列函数关系式并求解最值的能力,同时需要注意自变量的取值范围.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目