Question

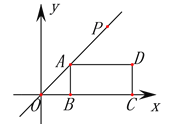
【题目】如图，在矩形ABCD中，AB=3cm，BC=6cm．点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．

（1）当t为何值时，四边形ABQP是矩形；

（2）当t为何值时，四边形AQCP是菱形；

（3）分别求出（2）中菱形AQCP的周长和面积．

Answer 1

【答案】（1）t=3，ABQP是矩形；（2）t=，AQCP是菱形；（3）周长为:15cm，面积为：（cm2）.

【解析】

（1）当四边形ABQP是矩形时，BQ=AP，据此求得t的值；
（2）当四边形AQCP是菱形时，AQ=AC，列方程求得运动的时间t；
（3）菱形的四条边相等，则菱形的周长=4AQ，面积=CQ×AB．

解：（1）由已知可得，BQ=DP=t，AP=CQ=6-t
在矩形ABCD中，∠B=90°，AD∥BC，
当BQ=AP时，四边形ABQP为矩形，
∴t=6-t，得t=3
故当t=3s时，四边形ABQP为矩形．
（2）AD∥BC，AP=CQ=6-t，

∴四边形AQCP为平行四边形
∴当AQ=CQ时，四边形AQCP为菱形
即＝6t时，四边形AQCP为菱形，解得t=，
故当t=s时，四边形AQCP为菱形．
（3）当t=时，AQ=，CQ=，
则周长为：4AQ=4×=15cm
面积为：CQAB＝×3＝．