题目内容
【题目】(10)已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O 相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O 相交于点E、F时,若∠DAE=18°,求∠BAF的大小.

【答案】(1)30°;(2)18°.
【解析】试题分析:(1)如图①,首先连接OC,由当直线l与⊙O相切于点C,AD⊥l于点D.易证得OC∥AD,继而可求得∠BAC=∠DAC=30°;
(2)如图②,连接BF,由AB是⊙O的直径,由直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,求得∠B的度数,继而求得答案.
试题解析:解:(1)如图①,连接OC,∵直线l与⊙O相切于点C,∴OC⊥l,∵AD⊥l,∴OC∥AD,∴∠OCA=∠DAC,∵OA=OC,∴∠BAC=∠OCA,∴∠BAC=∠DAC=30°;
(2)如图②,连接BF,∵AB是⊙O的直径,∴∠AFB=90°,∴∠BAF=90°﹣∠B,∴∠AEF=∠ADE+∠DAE=90°+18°=108°,在⊙O中,四边形ABFE是圆的内接四边形,∴∠AEF+∠B=180°,∴∠B=180°﹣108°=72°,∴∠BAF=90°﹣∠B=90°﹣72°=18°.
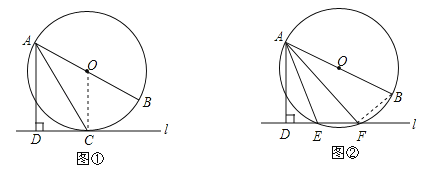

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目