��Ŀ����
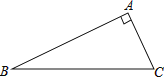
����Ŀ����ͼ�ף��ڡ�ABC�У���ACBΪ��ǣ���DΪ����BC��һ���㣬����AD����ADΪһ������AD���Ҳ�������ֱ��������ADE��AD=AE����DAE=90.����������⣺
(1) ���AB=AC����BAC=90��
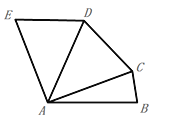
�ٵ���D���߶�BC��ʱ�����B���غϣ�����ͼ�ң��߶�CE��BD֮���λ�ù�ϵΪ��������ϵΪ��������֤����
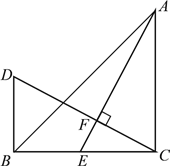
�ڵ���D���߶�BC���ӳ�����ʱ����ͼ�������еĽ����Ƿ���Ȼ������Ϊʲô��

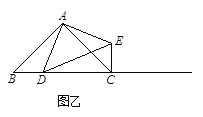
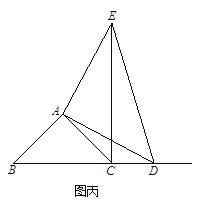
(2) ���AB��AC����BAC��90����D���߶�BC���˶���
��̽��������ABC����һ��ʲô����ʱ��CE��BD����C��E�غϳ��⣩��������Ӧ��ͼ�Σ���˵�����ɣ�
���𰸡�������
�������������������1���ٸ��ݡ�BAD=��CAE��BA=CA��AD=AE��������SAS��֤����ABD�ա�ACE������ȫ�����������ʵó���Ӧ����ȣ���Ӧ����ȣ����ɵõ��߶�CE��BD֮��Ĺ�ϵ�����ȸ�����SAS��֤����ABD�ա�ACE���ٸ���ȫ�����������ʵó���Ӧ����ȣ���Ӧ����ȣ����ɵõ����еĽ�����Ȼ������
��2���ȹ���A��AG��AC��BC�ڵ�G����������Ҫ���ͼ�Σ��ٽ��ͼ���ж���GAD�ա�CAE���ó���Ӧ����ȣ����ɵó����ۣ�
�����������1����CE��BDλ�ù�ϵ��CE��BD��������ϵ��CE=BD.
���ɣ���ͼ��,

�ߡ�BAD=90����DAC,��CAE=90����DAC��
���BAD=��CAE.
��BA=CA��AD=AE��
����ABD����ACE(SAS)
���ACE=��B=45����CE=BD.
�ߡ�ACB=��B=45����
���ECB=45��+45��=90������CE��BD.
�ʴ�Ϊ��CE��BD��CE=BD.
�ڵ���D��BC���ӳ�����ʱ,�ٵĽ����Գ���.
��ͼ��,

�ߡ�DAE=90��,��BAC=90����
���DAE=��BAC��
���DAB=��EAC��
��AB=AC��AD=AE��
����DAB����EAC��
��CE=BD���ҡ�ACE=��ABD.
�ߡ�BAC=90����AB=AC��
���ABC=45����
���ACE=45����
���BCE=��ACB+��ACE=90����
��CE��BD��
��2����ͼ����ʾ,����BCA=45��ʱ,CE��BD.
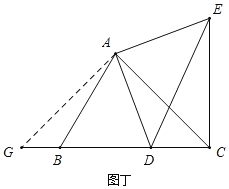
���ɣ�����A��AG��AC��BC�ڵ�G��
��AC=AG,��AGC=45����
����ACG�ǵ���ֱ�������Σ�
�ߡ�GAD+��DAC=90��=��CAE+��DAC��
���GAD=��CAE��
�֡�DA=EA��
����GAD����CAE��
���ACE=��AGD=45����
���BCE=��ACB+��ACE=90����
��CE��BD.

 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�