题目内容
【题目】我们规定:函数y=![]() (a、b、k是常数,k≠ab)叫奇特函数.当a=b=0时,奇特函数y=
(a、b、k是常数,k≠ab)叫奇特函数.当a=b=0时,奇特函数y=![]() 就是反比例函数y=
就是反比例函数y=![]() (k是常数,k≠0).
(k是常数,k≠0).
(1)如果某一矩形两边长分别是2和3,当它们分别增加x和y后,得到新矩形的面积为8.求y与x之间的函数表达式,并判断它是否为奇特函数;
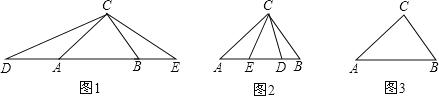
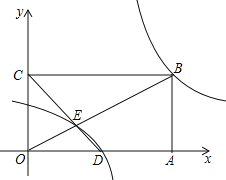
(2)如图,在平面直角坐标系xOy中,矩形OABC的顶点A、C坐标分别为(6,0)、(0,3),点D是OA中点,连接OB、CD交于E,若奇特函数y=![]() 的图象经过点B、E,求该奇特函数的表达式;
的图象经过点B、E,求该奇特函数的表达式;
(3)把反比例函数y=![]() 的图象向右平移4个单位,再向上平移 个单位就可得到(2)中得到的奇特函数的图象;
的图象向右平移4个单位,再向上平移 个单位就可得到(2)中得到的奇特函数的图象;
(4)在(2)的条件下,过线段BE中点M的一条直线l与这个奇特函数图象交于P,Q两点(P在Q右侧),如果以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
【答案】(1)y=![]() 是奇特函数.(2)奇特函数的表达式为y=
是奇特函数.(2)奇特函数的表达式为y=![]() .(3)2,见解析(4)P在原坐标系中的坐标为(4+2
.(3)2,见解析(4)P在原坐标系中的坐标为(4+2![]() +4,
+4,![]() ﹣2+2)即(2
﹣2+2)即(2![]() +8,
+8,![]() ).
).
【解析】
试题分析:(1)只需运用矩形的面积公式就可求出函数关系式,从而解决问题;
(2)可先求出直线OB和直线CD的解析式,求出它们的交点E的坐标,然后只需运用待定系数法就可解决问题;
(3)只需将(2)中所求的奇特函数y=![]() 转化为y=2+
转化为y=2+![]() ,就可解决问题;
,就可解决问题;
(4)将坐标原点平移到点M的位置,构建新的坐标系,在新的坐标系中,分点P在点B的左边和右边两种情况讨论,只需先求出点P在新坐标系下的坐标,就可求出点P在原坐标系下的坐标.
解:(1)由题意得:(2+x)(3+y)=8.
即3+y=![]() ,
,
∴y=![]() ﹣3=
﹣3=![]() .
.
根据定义,y=![]() 是奇特函数.
是奇特函数.
(2)如图1,

由题意得:B(6,3)、D(3,0),
设直线OB的解析式为y=mx,
则有6m=3,
解得:m=![]() ,
,
∴直线OB的解析式为y=![]() x.
x.
设直线CD的解析式为y=kx+b,
![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为y=﹣x+3.
解方程组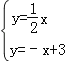 ,得
,得
![]() ,
,
∴点E(2,1).
将点B(6,3)和E(2,1)代入y=![]() 得
得
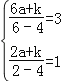 ,
,
解得:![]() ,
,
∴奇特函数的表达式为y=![]() .
.
(3)∵y=![]() =
=![]() =2+
=2+![]() .
.
∴把反比例函数y=![]() 的图象向右平移4个单位,再向上平移2个单位,
的图象向右平移4个单位,再向上平移2个单位,
就可得到奇特函数y=![]() 的图象;
的图象;
故答案为:2.
(4)满足条件的点P的坐标为(2![]() ,
,![]() +4)或(2
+4)或(2![]() +8,
+8,![]() ).
).
提示:①若点P在点B的左边,如图2①,
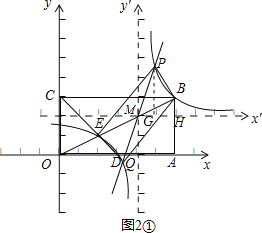
以点M为原点,构建如图2①所示的新坐标系,
在该坐标系下该奇特函数的解析式为y′=![]() ,点B的新坐标为(2,1).
,点B的新坐标为(2,1).
∵直线PQ与双曲线y′=![]() 都是以点M为对称中心的中心对称图形,
都是以点M为对称中心的中心对称图形,
∴MP=MQ.
∵MB=ME,
∴四边形BPEQ是平行四边形,
∴SBPEQ=4S△BMP=16,
∴S△BMP=4.
过点P作PG⊥x′轴于G,过点B作BH⊥x′轴于H,
根据反比例函数比例系数的几何意义可得:
S△PGM=S△BHM=![]() ×2=1,
×2=1,
∴S△BMP=S△PGM+S梯形BHGP﹣S△BHM=S梯形BHGP=4,
设点P在新坐标系中的坐标为(x′,![]() ),
),
则有S梯形BHGP=![]() (1+
(1+![]() )(2﹣x′)=4,
)(2﹣x′)=4,
解得x1′=﹣4﹣2![]() (舍去),x2′=﹣4+2
(舍去),x2′=﹣4+2![]() ,
,
当x=﹣4+2![]() 时,
时,![]() =
=![]() =
=![]() +2,
+2,
即点P在新坐标系中的坐标为(﹣4+2![]() ,
,![]() +2),
+2),
∴点P在原坐标系中的坐标为(﹣4+2![]() +4,
+4,![]() +2+2)即(2
+2+2)即(2![]() ,
,![]() );
);
②若点P在点B的右边,如图2②,
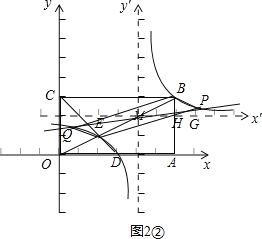
同理可得:
点P在原坐标系中的坐标为(4+2![]() +4,
+4,![]() ﹣2+2)即(2
﹣2+2)即(2![]() +8,
+8,![]() ).
).

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案