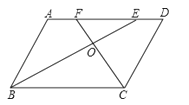
题目内容
【题目】如图，△ABC中，AB=AC， 
BAC=40°，将△ABC绕点A按逆时针方向旋转100°得到△ADE，连接BD，CE交于点F.
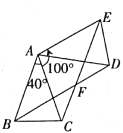
(1)求证：△ABD≌△ACE；
(2)求证：四边形ABFE是菱形．
【答案】（1）证明见试题解析；（2）证明见试题解析．
【解析】试题分析：（1）根据旋转角求出∠BAD=∠CAE，然后利用“边角边”证明△ABD和△ACE全等．
（2）根据对角相等的四边形是平行四边形，可证得四边形ABFE是平行四边形，然后依据邻边相等的平行四边形是菱形，即可证得．
试题解析：（1）∵△ABC绕点A按逆时针方向旋转100°，∴∠BAC=∠DAE=40°，∴∠BAD=∠CAE=100°，又∵AB=AC，∴AB=AC=AD=AE，在△ABD与△ACE中，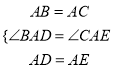 
，∴△ABD≌△ACE（SAS）；
（2）∵∠BAD=∠CAE=100°AB=AC=AD=AE，∴∠ABD=∠ADB=∠ACE=∠AEC=40°，∵∠BAE=∠BAD+∠DAE=140°，∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°，∴∠BAE=∠BFE，∴四边形ABFE是平行四边形，∵AB=AE，∴平行四边形ABFE是菱形．
【题目】某校八年级共有150名男生，从中随机抽取30名男生在“阳光体育活动”启动日进行“引体向上”测试，下表是测试成绩记录（单位：个）：
3 | 2 | 1 | 2 | 3 | 3 | 5 | 2 | 2 | 4 |
2 | 4 | 2 | 5 | 2 | 3 | 4 | 4 | 1 | 3 |
3 | 2 | 5 | 1 | 4 | 2 | 3 | 1 | 2 | 4 |
（1）我们已经会列频数分布表、画条形统计图、折线统计图和扇形统计图．为了能让体育老师一目了然知道整个测试情况，请你选择一种合适的统计表或统计图整理表示上述数据；
（2）观察分析（1）中的统计表或统计图，请你写出两条从中获得的信息：
（3）规定八年级男生“引体向上”4个及以上为合格．若学校准备对“引体向上”不合格的男生提出锻炼建议，试估计要对八年级多少名男生提出这项建议？
