题目内容
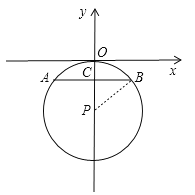
【题目】在平面直角坐标系中，点P的坐标为（0，﹣5），以P为圆心的圆与x轴相切，⊙P的弦AB（B点在A点右侧）垂直于y轴，且AB=8，反比例函数
（k≠0）经过点B，则k=______．
【答案】﹣8或﹣32．
【解析】解：设线段AB交y轴于点C，当点C在点P的上方时，连接PB，如图，∵⊙P与x轴相切，且P（0，﹣5），∴PB=PO=5，∵AB=8，∴BC=4，在Rt△PBC中，由勾股定理可得PC=
=3，∴OC=OP﹣PC=5﹣3=2，∴B点坐标为（4，﹣2），∵反比例函数
（k≠0）经过点B，∴k=4×（﹣2）=﹣8；
当点C在点P下方时，同理可求得PC=3，则OC=OP+PC=8，∴B（4，﹣8），∴k=4×（﹣8）=﹣32；
综上可知k的值为﹣8或﹣32，故答案为：﹣8或﹣32．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
