题目内容
 25、(1)如图1,四边形ABCD中,AB=CB,ABC=60°,∠ADC=120°,请你猜想线段DA,DC之和与线段BD的数量关系,并证明你的结论;
25、(1)如图1,四边形ABCD中,AB=CB,ABC=60°,∠ADC=120°,请你猜想线段DA,DC之和与线段BD的数量关系,并证明你的结论;(2)如图2,四边形ABCD中,AB=BC,∠ABC=60°,若点P为四边形ABCD内一点,且∠APD=120°,请你猜想线段PA,PD,PC之和与线段BD的数量关系,并证明你的结论.
分析:(1)可通过构建全等三角形将所求的三条线段进行转换,延长CD至E,使DE=DA.那么CD+AD=CE了,只要证明BD和CE的关系即可,根据∠ADC=120°,那么∠ADE=60°,因为AD=DE,那么三角形ADE是个等边三角形,AD=DE,∠E=60°.根据AB=AC,∠ABC=60°,那么三角形ABC是个等边三角形,那么AB=AC,
∠BAC=60°,那么∠BAD=60+∠CAD=∠EAC,因此根据求出∠EAC=∠BAD,AB=AC,AD=AE,三角形BAD就和三角形CAE全等了,因此BD=CE=CD+DE=CD+AD.
(2)我们可参照(1)在四边形ABCD外侧作正三角形AB′D,然后连接AC,根据(1)得出那么三角形ABC和AB′D都是等边三角形,那么AB=AC,AB′=AD,∠BAD=∠B′AC=60°+∠CAD,因此三角形BAD和CAB′全等,那么B′D=BD,由(1)得出B′P=PA+PD,BD=PA+PD那么我们连接B′C,分两种情况进行讨论①P在B′C上,那么B′C=B′P+PC=AP+PD+PC=BD.
②如果点P不在B′C上面,那么B′C<B′P+PC,即BD<PD+AD+PC.
∠BAC=60°,那么∠BAD=60+∠CAD=∠EAC,因此根据求出∠EAC=∠BAD,AB=AC,AD=AE,三角形BAD就和三角形CAE全等了,因此BD=CE=CD+DE=CD+AD.
(2)我们可参照(1)在四边形ABCD外侧作正三角形AB′D,然后连接AC,根据(1)得出那么三角形ABC和AB′D都是等边三角形,那么AB=AC,AB′=AD,∠BAD=∠B′AC=60°+∠CAD,因此三角形BAD和CAB′全等,那么B′D=BD,由(1)得出B′P=PA+PD,BD=PA+PD那么我们连接B′C,分两种情况进行讨论①P在B′C上,那么B′C=B′P+PC=AP+PD+PC=BD.
②如果点P不在B′C上面,那么B′C<B′P+PC,即BD<PD+AD+PC.
解答: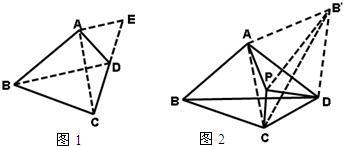 解:(1)如图1,延长CD至E,使DE=DA.连接AC.
解:(1)如图1,延长CD至E,使DE=DA.连接AC.
∵∠ADC=120°,
∴∠ADE=60°.
∵AD=DE,
∴△EAD是等边三角形.
∴AE=AE,∠DAE=60°.
∴AB=AC,∠ABC=60°,
∵∠BAD=60°+∠CAD,∠EAC=60°+∠CAD,
∴∠BAD=∠CAE.
∴△BAD≌△CAE.
故AD+CD=DE+CD=CE=BD.
(2)如图2,在四边形ABCD外侧作正三角形AB′D,连接AC,
那么三角形AB′D和三角形ABC都是等边三角形,
∴AB=AC,AB′=AD.
∵∠BAD=∠B′AC=60°+∠CAD,
∴△AB′C≌△ADB,得B′C=DB.
∵四边形AB′DP符合(1)中条件,
∴B′P=AP+PD.
连接B′C,
(ⅰ)若满足题中条件的点P在B′C上,
则B′C=PB′+PC,
∴B′′C=AP+PD+PC.
∴BD=PA+PD+PC.
(ⅱ)若满足题中条件的点P不在B′C上,
∵B′C<PB′+PC,
∴B′C<AP+PD+PC.
∴BD<PA+PD+PC.
综上,BD≤PA+PD+PC.
 解:(1)如图1,延长CD至E,使DE=DA.连接AC.
解:(1)如图1,延长CD至E,使DE=DA.连接AC.∵∠ADC=120°,
∴∠ADE=60°.
∵AD=DE,
∴△EAD是等边三角形.
∴AE=AE,∠DAE=60°.
∴AB=AC,∠ABC=60°,
∵∠BAD=60°+∠CAD,∠EAC=60°+∠CAD,
∴∠BAD=∠CAE.
∴△BAD≌△CAE.
故AD+CD=DE+CD=CE=BD.
(2)如图2,在四边形ABCD外侧作正三角形AB′D,连接AC,
那么三角形AB′D和三角形ABC都是等边三角形,
∴AB=AC,AB′=AD.
∵∠BAD=∠B′AC=60°+∠CAD,
∴△AB′C≌△ADB,得B′C=DB.
∵四边形AB′DP符合(1)中条件,
∴B′P=AP+PD.
连接B′C,
(ⅰ)若满足题中条件的点P在B′C上,
则B′C=PB′+PC,
∴B′′C=AP+PD+PC.
∴BD=PA+PD+PC.
(ⅱ)若满足题中条件的点P不在B′C上,
∵B′C<PB′+PC,
∴B′C<AP+PD+PC.
∴BD<PA+PD+PC.
综上,BD≤PA+PD+PC.
点评:本题考查了全等三角形的判定,等边三角形的性质和三角形三边的关系等知识点,本题中利用全等三角形来进行线段的转换是解题的关键.

练习册系列答案
相关题目
 如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论: 如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.
如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.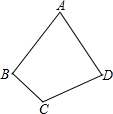 如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
 如图,凸四边形有
如图,凸四边形有