Question

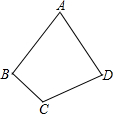如图是一块四边形的薄钢板，∠A=60°，∠C=120°，AB=AD．
（1）能否先沿一条对角线将钢板切割成两块，再焊接成一块与原钢板面积相同的三角形钢板？若能，请说明切割、焊接的方法，用虚线画出示意图，并说明焊接的钢板是什么三角形；若不能，请说明理由；
（2）若BC=1m，CD=3m，求这块钢板的面积．

Answer 1

分析：（1）利用四边形的内角和等于360度可得∠ABC+∠D=180°，所以可沿对角线AC切割后，把△ABC与△ADC放在AB两侧，使AD与AB重合，点C落到点C′，再重新焊接即可；
（2）利用（1）的方法，可以把△ADC绕着A点旋转到△AC′B，就使原四边形转化为ACC′，其中AC=AC′，∠CAC'=60°，△ACC'是等边三角形，原四边形的面积就等于该三角形的面积．

解答：解：（1）由已知，得∠ABC+∠D=180°，如图所示，沿对角线AC切割后，把△ABC与△ADC放在AB两侧，使AD与AB重合，点C落到点C‘，再重新焊接，这时，∠ABC+∠ABC′=∠ABC+∠D=180°；

（2）把△ADC绕着A点旋转到△ACnB，就使原四边形转化为△ACC’，
其中AC=AC′，且有∠CAC'=∠CAB+∠C'AB=∠CAB+∠CAD=60°，
所以△ACC'是等边三角形，CC′=BC+BC’=BC+CD=4，
于是可以求得S△ACCn=4

3

(m2)，也就是钢板面积．

点评：本题需仔细分析题意，结合图形，利用旋转即可解决问题．