题目内容
【题目】如图,在矩形ABCD中,AB=10cm,BC=4cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D停止,当运动时间为秒时,△MBN为等腰三角形. 
【答案】![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]()
【解析】解:①如图1, 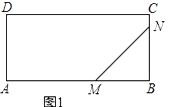
点M在AB上,点N在BC上时,t<4,BM=10﹣2t,BN=t,
∵BM=BN,
∴10﹣2t=t,
解得t= ![]() ,
,
②如图2,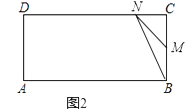
点M在BC上,点N在CD上时,5<t<7,BM=2t﹣10,CM=4﹣(2t﹣10)=14﹣2t,
CN=t﹣4,
在Rt△MCN中,MN2=(14﹣2t)2+(t﹣4)2 ,
∵BM=MN,
∴(2t﹣10)2=(14﹣2t)2+(t﹣4)2 ,
整理得,t2﹣24t+112=0,
解得t1=12﹣4 ![]() ,t2=12+4
,t2=12+4 ![]() (舍去),
(舍去),
③如图3,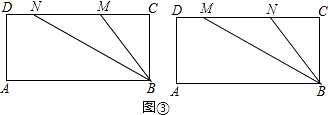
点M、N都在C、D上时,t>7,若点M在点N的右边,则CM=2t﹣14,MN=t﹣(2t﹣14)=14﹣2t,
此时BM2=(2t﹣14)2+42 ,
∵BM=MN,
∴(2t﹣14)2+42=(14﹣2t)2 , 无解,
若点M在点N的左边,则CN=t﹣4,
MN=(2t﹣14)﹣(t﹣4)=t﹣10,
此时BN2=(t﹣4)2+42 ,
∵BN=MN,
∴(t﹣4)2+42=(t﹣10)2 ,
整理得,t= ![]() (不符合题意,舍去),
(不符合题意,舍去),
④如图④,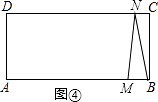
点M在AB上,点N在CD上时,BM=10﹣2t,CN=t﹣4,
由等腰三角形三线合一的性质,CN= ![]() BM,
BM,
所以,t﹣4= ![]() (10﹣2t),
(10﹣2t),
解得t= ![]() ,
,
综上所述,当运动时间为 ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() 秒时,△MBN为等腰三角形.
秒时,△MBN为等腰三角形.
故答案为: ![]() 或(12﹣4
或(12﹣4 ![]() )或
)或 ![]() .
.
分①点M在AB上,点N在BC上时,BM=BN,列出方程其解即可,②点M在BC上,点N在CD上时,表示出BM、CM、CN,再根据勾股定理列式表示出MN2 , 然后根据BM=MN列出方程其解即可;③点M、N都在C、D上时,表示出MN、CM,再根据勾股定理分两种情况列式表示出BM(或BN),然后根据BM=MN(或BN=MN)列出方程求解即可,④点M在AB上,点N在CD上时,根据等腰三角形的性质,CN= ![]() BM,然后列式求解即可.
BM,然后列式求解即可.