题目内容
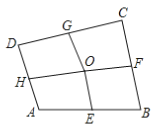
【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、8,则四边形DHOG的面积是________.
【答案】7
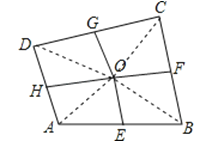
【解析】解：连接OC，OB，OA，OD．∵E、F、G、H依次是各边中点，∴△AOE和△BOE等底等高，∴S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE．∵S四边形AEOH=4，S四边形BFOE=5，S四边形CGOF=8，∴4+8=5+S四边形DHOG，解得：S四边形DHOG=7．故答案为：7．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
【题目】某服装厂计划生产A，B两款校服共500件，这两款校服的成本、售价如表所示：
类别 | 成本（元/件） | 售价（元/件） |
A款 | 30 | 45 |
B款 | 50 | 70 |
（1）求校服厂家销售完这批校服时所获得的利润y（元）与A款校服的生产数量x（件）之间的函数关系．
（2）若厂家计划B款校服的生产数量不超过A款校服的生产数量的4倍，应怎样安排生产才能使校服厂家在销售完这批校服时获得利润最多？此时获得利润为多少元？
