Question

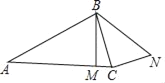
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，AB＝4，点M是直角边AC上一动点，连接BM，并将线段BM绕点B逆时针旋转60°得到线段BN，连接CN．则在点M运动过程中，线段CN长度的最大值是_____，最小值是_____．

Answer 1

【答案】2， 1

【解析】

将Rt△ABC绕点B旋转60°，得到Rt△FBE，则△ABC≌△FBE，B，C，F三点在同一条直线上，点N的轨迹在线段EF上，连接CE，则当点N与点E重合时CN的长度最大，当CN⊥EF于点N时，CN的长度最小，可利用解直角三角形等求出其最大值与最小值．

在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，AB＝4，

∴BC＝AB＝2，

将Rt△ABC绕点B旋转60°，得到Rt△FBE，

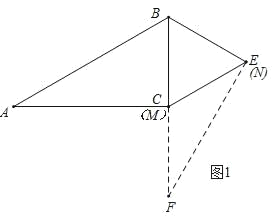
则△ABC≌△FBE，B，C，F三点在同一条直线上，点N的轨迹在线段EF上，

∴∠E＝∠ACB＝90°，∠F＝∠BAC＝30°，BF＝AB＝4，

∴CF＝BF﹣BC＝2，

∴点C为BF的中点，

连接CE，则当点N与点E重合时CN的长度最大，

其最大值为：CE＝BF＝2；

如图2，当CN⊥EF于点N时，CN的长度最小，

∵CE＝BF＝CF，

∴点N为EF的中点，

∴CN＝BE＝BC＝1，

故答案为：2，1．