题目内容
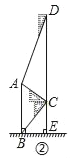
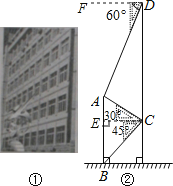
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

【答案】雕塑AB的高度约为6.8米.
【解析】试题分析:首先证明△ADC是直角三角形,求出AC.在Rt△ACE中,求出AE.在Rt△BCE中,求出BE,即可解决问题.
试题解析:解:过点C作CE⊥AB于E.∵∠ADC=90°﹣60°=30°,∠ACD=90°﹣30°=60°,∴∠CAD=90°.∵CD=10,∴AC=![]() CD=5.
CD=5.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,∴AE=![]() AC=
AC=![]() ,CE=ACcos∠ACE=5cos30°=
,CE=ACcos∠ACE=5cos30°=![]() .
.
在Rt△BCE中,∵∠BCE=45°,∴BE=CE=![]() ,∴AB=AE+BE=
,∴AB=AE+BE=![]() +
+![]() =
=![]() (
( ![]() +1)≈6.8(米).
+1)≈6.8(米).
答:雕塑AB的高度约为6.8米.

 阅读快车系列答案
阅读快车系列答案【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
【题目】某中学数学活动小组为了调查居民的用水情况,从某社区的![]() 户家庭中随机抽取了
户家庭中随机抽取了![]() 户家庭的月用水量,结果如下表所示:
户家庭的月用水量,结果如下表所示:
月用水量(吨) |
|
|
|
|
|
|
|
户数 |
|
|
|
|
|
|
|
![]() 求这
求这![]() 户家庭月用水量的平均数、众数和中位数;
户家庭月用水量的平均数、众数和中位数;
![]() 根据上述数据,试估计该社区的月用水量;
根据上述数据,试估计该社区的月用水量;
![]() 由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为
由于我国水资源缺乏,许多城市常利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为![]() (吨),家庭月用水量不超过
(吨),家庭月用水量不超过![]() (吨)的部分按原价收费,超过
(吨)的部分按原价收费,超过![]() (吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由.
(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合适?简述理由.