题目内容
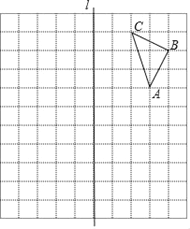
【题目】如图,在平面直角坐标系中,△ABC的顶点A的坐标为(0,﹣1),顶点B在x轴的负半轴上,顶点C在y轴的正半轴上,且∠ABC=90°,∠ACB=30°,线段OC的垂直平分线分别交OC,BC于点D,E.
(1)点C的坐标;
(2)点P为线段ED的延长线上的一点,连接PC,PA,设点P的横坐标为t,△ACP的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点F为线段BC的延长线上一点,连接OF,若OF=CP,求∠OFP的度数.
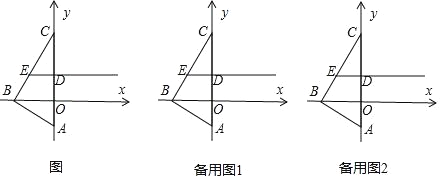
【答案】(1)C(0,3);(2)S=2t;(3)60°.
【解析】
(1)根据直角三角形30度角的性质分别计算AB和AC的长,可得OC的长,写出点C的坐标;
(2)根据三角形面积公式得:S△ACP=![]() ×AC×DP=
×AC×DP=![]() ×4×t=2t;
×4×t=2t;
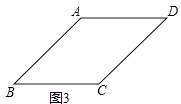
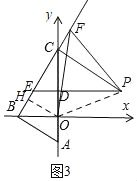
(3)如图3,过点O作OH⊥BC于H,证明Rt△OHF≌Rt△ODP,得∠HFO=∠DPO,再证明△FOP是等边三角形,则∠OFP=60°.
(1)∵∠ABC=90°,
∴∠CBO+∠ABO=90°,
∵∠CBO+∠ACB=90°,
∴∠ABO=∠ACB,
∴∠ACB=30°,
∴∠ABO=30°,
在Rt△AOB中,∵∠ABO=30°,
∴AB=2OA,
在Rt△ABC中,∠ACB=30°,
∴AC=2AB,
∵A(0,﹣1),
∴OA=1,
∴AB=2,AC=4,
∴OC=AC﹣OA=4﹣1=3,
∴C(0,3);
(2)∵DE所在直线为线段OC的垂直平分线,
∴PD⊥OC,
∵点P的横坐标为t,
∴PD=t,
∵AC=4,
∴S△ACP=![]() =2t,
=2t,
即S=2t;
(3)如图3,过点O作OH⊥BC于H,连接OP,
在Rt△CHO中,∵∠HCO=30°,
∴OH=![]() OC,
OC,
∵OD=![]() OC,
OC,
∴OH=OD,
∵PE所在直线为线段CD的垂直平分线,
∴PC=PO,
∴OF=CP,
∴PO=FO,
在Rt△OHF和Rt△ODP中,
∵![]() ,
,
∴Rt△OHF≌Rt△ODP(HL),
∴∠HFO=∠DPO,
∴∠FEP+∠HFO=∠FOP+∠DPO,
∴∠FEP=∠FOP,
∵∠FEP=60°,
∴∠FOP=60°,
∴△FOP是等边三角形,
∴∠OFP=60°.

【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
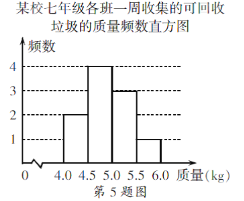
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.