题目内容
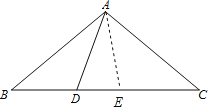
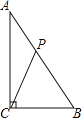
【题目】在△ABC中，已知D为直线BC上一点，若∠ABC=x°，∠BAD=y°．
（1）若CD=CA=AB，请求出y与x的等量关系式；
（2）当D为边BC上一点，并且CD=CA，x=40，y=30时，则AB AC（填“=”或“≠”）；
（3）如果把（2）中的条件“CD=CA”变为“CD=AB”，且x，y的取值不变，那么（1）中的结论是否仍成立？若成立请写出证明过程，若不成立请说明理由．
【答案】（1）3x+2y=180；（2）=；（3）成立．理由见解析
【解析】
试题分析：（1）由CD=CA，可表示出∠ADC的度数，又由三角形外角的性质，可得∠ADC=∠B+∠BAD，则可得方程：90﹣
x=x+y，继而求得答案；
（2）由CD=CA，x=40，y=30，首先可求得∠ADC的度数，继而证得CD=CA，则可求得∠C=∠B=40°，证得AB=AC；
（3）首先在BC上取点E，使BE=CD=AB，连接AE，易证得AD=AE，继而可得△ADB≌△AEC（SAS），则可证得结论．
解：（1）∵∠ABC=x°，CA=AB，
∴∠C=∠ABC=x°，
∵CD=CA，
∴∠ADC=∠CAD=
=90°﹣x°，
∵∠ADC=∠B+∠BAD，
∴90﹣
x=x+y，
即：3x+2y=180；
（2）∵CD=CA，∠ABC=x°=40°，∠BAD=y°=30°，
∴∠ADC=∠ABC+∠BAD=70°，
∵CD=CA，
∴∠CAD=∠CDA=70°，
∴∠C=40°，
∴∠C=∠ABC，
∴AB=AC；
故答案为：=；
（3）成立．
理由：在BC上取点E，使BE=CD=AB，连接AE，
则∠AEB=∠EAB=（180°﹣40°）=70°，
∴∠AEB=∠ADE=70°，
∴AD=AE，
∴∠ADB=∠AEC=180°﹣70°=110°，
∵BD=BE﹣DE，CE=CD﹣DE，
∴BD=EC，
在△ADB和△AEC中，
，
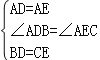∴△ADB≌△AEC（SAS），
∴AB=AC．
