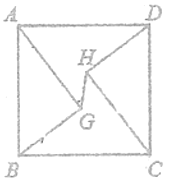
题目内容
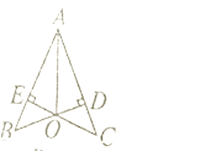
【题目】如图,![]() 是
是![]() 的外角,
的外角,![]() 的平分线所在的直线分别与
的平分线所在的直线分别与![]()
![]() 的平分线
的平分线![]() 交于点
交于点![]() .
.
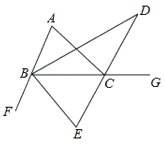
![]() 若
若![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() 求
求![]() ;
;
![]() 连接
连接![]() 若
若![]() 则
则![]() _
_
【答案】(1)∠D=35°;(2)∠E=90°![]() α;(3)
α;(3)![]()
【解析】
(1)由角平分线的定义得到∠DCG=![]() ∠ACG,∠DBC=
∠ACG,∠DBC=![]() ∠ABC,然后根据三角形外角的性质求出2∠DCG=∠A+2∠DBC,2∠DCG=2∠D+2∠DBC,等量代换即可得出答案;
∠ABC,然后根据三角形外角的性质求出2∠DCG=∠A+2∠DBC,2∠DCG=2∠D+2∠DBC,等量代换即可得出答案;
(2)由(1)知∠D=![]() ∠A=
∠A=![]() α,求出∠DBE=90°,即可求得∠E;
α,求出∠DBE=90°,即可求得∠E;
(3)如图,连接AD,过点D作DN⊥BG于N,DM⊥BA交BA的延长线于M,过点D作DQ⊥AC于Q,根据角平分线的判定和性质证得AD是∠MAC的角平分线,然后利用三角形外角的性质求出∠MAD=![]() ∠MAC=
∠MAC=![]() ,∠MAD=∠ABD+∠ADB=
,∠MAD=∠ABD+∠ADB=![]() +∠ADB,等量代换即可求出答案.
+∠ADB,等量代换即可求出答案.
解:(1)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=![]() ∠ACG,∠DBC=
∠ACG,∠DBC=![]() ∠ABC,
∠ABC,
∵∠ACG=∠A+∠ABC,
∴2∠DCG=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=![]() ∠A=35°;
∠A=35°;
(2)由(1)知∠D=![]() ∠A=
∠A=![]() α,
α,
∵∠DBE=∠DBC+∠CBE=![]() ∠ABC+
∠ABC+![]() ∠CBF=
∠CBF=![]() (∠ABC+∠CBF)=
(∠ABC+∠CBF)=![]() ×180°=90°,
×180°=90°,
∴∠E=90°-∠D=90°![]() α;
α;
(3)如图,连接AD,过点D作DN⊥BG于N,DM⊥BA交BA的延长线于M,过点D作DQ⊥AC于Q,
∵BD是∠ABC的平分线,CD是∠ACG的平分线,
∴DM=DN,DQ=DN,
∴DM=DQ,
∵DM⊥AM,DQ⊥AC,
∴AD是∠MAC的角平分线,
∵∠MAC=∠ACB+∠ABC=β+∠ABC,
∴∠MAD=![]() ∠MAC=
∠MAC=![]() ,
,
又∵∠MAD=∠ABD+∠ADB=![]() +∠ADB,
+∠ADB,
∴![]() ,
,
∴![]() .
.