��Ŀ����
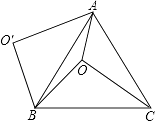
����Ŀ����ͼ1����������ABCD�У���E��AB��һ�㣬��F��AD�ӳ�����һ�㣬��DF=BE������CE��CF��
��1����֤��CE=CF��
��2����ͼ1�У�����G��AD�ϣ�����GCE=45�㣬��GE=BE+GD������Ϊʲô��
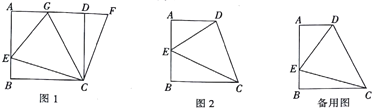
��3����������ѧ��֪ʶ�����ã�1������2������л��۵ľ��飬������и��⣬��ͼ2�����ı���ABCD�У�AD��BC��BC��AD������B=90�㣬AB=BC������DCE=45�㣮
����AE=6��DE=10����AB�ij���
����AB=BC=9��BE=3����DE�ij���
���𰸡���1��֤����������2��������3����12����7.5
��������
��1�����жϳ���B=��CDF�������жϳ���CBE�ա�CDE�����ɵó����ۣ�
��2�����жϳ���BCE=��DCF�������жϳ���ECF=��BCD=90�������ɵó���GCF=��GCE=45�����ó���ECG�ա�FCG���ɵó����ۣ�
��3�����жϳ�����ABCHΪ�����Σ������ó�AH=BC=AB��
�ٸ��ݹ��ɶ����ã�AD=8���ɣ�1����2��֪��ED=BE+DH����BE=x��������ʾ��DH=10-x����AH=AB�������̼��ɵó����ۣ�
���ɣ�1����2��֪��ED=BE+DH����DE=a��������ʾ��DH=a-3��AD=12-a��AE=6�����ݹ��ɶ�������������⼴�ɵó����ۣ�
��1����������ABCD��
��BC=CD����B=��ADC��
���B=��CDF��
��BE=DF��
���CBE�ա�CDF��
��CE=CF��
��2���������ɣ�1��֪����CBF�ա�CDE��
���BCE=��DCF��
���BCE+��ECD=��DCF+��ECD��
���ECF=��BCD=90�㣬
�ߡ�GCE=45�㣬
���GCF=��GCE=45�㣬
��CE=CF����GCE=��GCF��GC=GC��
���ECG�ա�FCG��
��GE=GF��
��GE=DF+GD=BE+GD��
��3����ͼ2������C��CH��AD��AD���ӳ�����H��
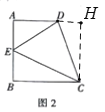
��AD��BC����B=90�㣬
���A=90�㣬
�ߡ�CHA=90�㣬
���ı���ABCHΪ���Σ�
��AB=BC��
�����ABCH������
��AH=BC=AB��
�١�AE=6��DE=10�����ݹ��ɶ����ã�AD=8��
�ߡ�DCE=45�㣬
�ɣ�1����2��֪��ED=BE+DH��
��BE=x��
��10+x=DH��
��DH=10-x��
��AH=AB��
��8+10-x=x+6��
��x=6��
��AB=12��
�ڡߡ�DCE=45�㣬
�ɣ�1����2��֪��ED=BE+DH��
��DE=a��
��a=3+DH��
��DH=a-3��
��AB=AH=9��
��AD=9-��a-3��=12-a��AE=AB-BE=6��
���ݹ��ɶ����ã�DE2=AD2+AE2��
������12-a��2+62=a2����a=7.5��
��DE=7.5��

 ������������ϵ�д�
������������ϵ�д�