Question

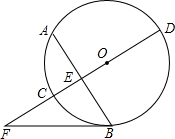如图，CD是⊙O的直径，弦AB⊥CD于E，F是DC延长线上的一点，连接BF．若AE=，EO=1，CF=2．
（1）求⊙O的半径．
（2）求证：直线BF是⊙O的切线．

Answer 1

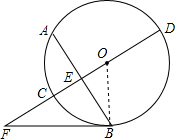解：（1）连接OB．
∵CD是⊙O的直径，弦AB⊥CD于E，
∴BE=AE=，∠OEB=90°，
在Rt△OEB中：OB===2，
∴⊙O的半径为2；

（2）∵CF=2，OC=B=2，
∴OF=OC+CG=4，
∴，，
∴，
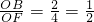∵∠EOB=∠BOF，
∴△OBE∽△OFB，
∴∠OBF=∠OEB=90°，
∴OB⊥BF，
∴直线BF是⊙O的切线．
分析：（1）由CD是⊙O的直径，弦AB⊥CD于E，根据垂径定理，即可求得BE的长，然后由勾股定理，即可求得⊙O的半径OB的长．
（2）由CF=2即可求得OF的长，即可求得，又由∠BOE是公共角，即可得△OBE∽△OFB，则∠OBF=∠OEB=90°，继而证得直线BF是⊙O的切线．
点评：此题考查了垂径定理与圆的切线的判定，以及勾股定理等知识．此题难度不大，解题的关键是数形结合思想的应用与辅助线的作法．