题目内容
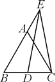
【题目】如图,已知AB⊥BD,CD⊥BD
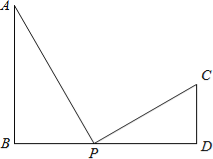
(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB=m,CD=n,BD=l,请问m,n,l满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
【答案】解:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若![]() ,则
,则![]() ,解得:x=
,解得:x=![]() 。
。
②若![]() ,则
,则![]() ,即x2﹣10x+36=0,△=(﹣10)2﹣4×1×36<0,此方程无解。
,即x2﹣10x+36=0,△=(﹣10)2﹣4×1×36<0,此方程无解。
∴存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为![]() 。
。
(2)在BD上存在2个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若![]() ,则
,则![]() ,解得:x=
,解得:x=![]() 。
。
②若![]() ,则
,则![]() ,即x2﹣12x+36=0,解得:x1=x2=6。
,即x2﹣12x+36=0,解得:x1=x2=6。
∴存在2个点P,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为![]() 或6。
或6。
(3)在BD上存在3个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若![]() ,则
,则![]() ,解得:x=
,解得:x=![]() 。
。
②若![]() ,则
,则![]() ,即x2﹣15x+36=0,解得:x1=3,x2=12。
,即x2﹣15x+36=0,解得:x1=3,x2=12。
∴存在3个点P ,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为![]() 或3或12。
或3或12。
(4)设BP=x,
∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°。
∴当![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似。
①若![]() ,则
,则![]() ,解得:x=
,解得:x=![]() 。
。
②若![]() ,则
,则![]() ,即x2﹣lx+mn=0。
,即x2﹣lx+mn=0。
∵△=(﹣l)2﹣4×1×mn=l2﹣4mn,
∴当l2﹣4mn<0时,方程没有实数根;当l2﹣4mn=0时,方程有2个相等的实数根;当l2﹣4mn>0时,方程有2个不相等的实数根。
∴当l2﹣4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点;
当l2﹣4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点;
当l2﹣4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点。
【解析】
(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
(2)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
(3)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出![]() 或
或![]() 时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可。
(4)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当![]() 或
或![]() 时使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入后根据根的判别式进行判断即可。
时使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入后根据根的判别式进行判断即可。