题目内容
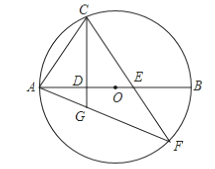
【题目】学完三角形的高后,小明对三角形与高线做了如下研究:如图,![]() 是
是![]() 中边
中边![]() 上的-点,过点
上的-点,过点![]() 、
、![]() 分别作、
分别作、![]() 、
、![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() 、
、![]() ,由
,由![]() 与
与![]() 的面积之和等于
的面积之和等于![]() 的面积,有等量关系式:
的面积,有等量关系式:![]() .像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.
.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.



图(1) 图(2)
(1)如图(1), 矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,求
,求![]() 的值;
的值;
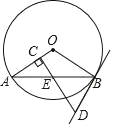
(2)如图(2),在![]() 中,角平分线
中,角平分线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
【答案】(1)![]() ;(2)4
;(2)4
【解析】
(1)由矩形的性质可得∠ABC=90°,AO=CO,BO=DO,由“等积法”可求解;
(2)由“等积法”可求OM=ON=1,通过证明四边形AMON是正方形,即可求解.
解:(1)如图,连接![]() ,
,
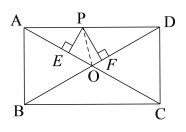
则由矩形性质有:
![]()
![]()
又![]()
∴![]()
∴![]()
解得:![]() ;
;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
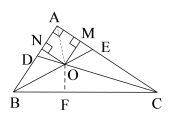
又![]() 是
是![]() 的角平分线,
的角平分线,![]() 、
、![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,
,
![]() ,
,![]()
![]()
在![]() 中,
中,![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
解得:![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
又![]()
![]() 矩形
矩形![]() 是正方形
是正方形
![]() 正方形
正方形![]() 的周长
的周长![]() .
.

练习册系列答案
相关题目