题目内容
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
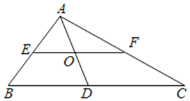
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

【答案】(1)∠C=56°;(2)∠AMF=∠ANG.证明见解析;(3)满足条件的旋转角为28°或56°或208°或236°.
【解析】
(1)利用三角形的内角和定理即可解决问题;
(2)结论:∠AMF=∠ANG.由翻折可知:∠B=∠F,∠C=∠DGN,由∠B+∠C=90°,推出∠BAC=90°,∠F+∠DGN=90°,推出∠BAD+∠CAD=90°,由∠BAD=∠F+∠AMF,∠CAD=∠DGN-∠ANG,推出∠F+∠AMF+∠DGN-∠ANG=90°,可得∠AMF=∠ANG;
(3)分两种情形①当∠PQB=90°时;②当∠BPQ=90°时.分别求解即可解决问题.
解:(1)如图1中,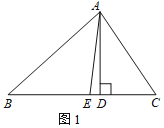
∵AD⊥BC,
∴∠ADB=∠ADC=90°
在Rt△AED中,∵∠EAD=7°,
∴∠AED=83°,
∵∠AED=∠B+∠BAE,∠B=42°,
∴∠BAE=∠CAE=41°,
∴∠BAC=82°,
∴∠C=180°-42°-82°=56°.
(2)结论:∠AMF=∠ANG.
理由:如图2中,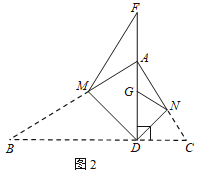
由翻折可知:∠B=∠F,∠C=∠DGN,
∵∠B+∠C=90°,
∴∠BAC=90°,∠F+∠DGN=90°,
∴∠BAD+∠CAD=90°,
∵∠BAD=∠F+∠AMF,∠CAD=∠DGN-∠ANG,
∴∠F+∠AMF+∠DGN-∠ANG=90°,
∴∠AMF=∠ANG.
(3)①如图3-1当∠PQB=90°时,
∵∠B=∠F′=28°,
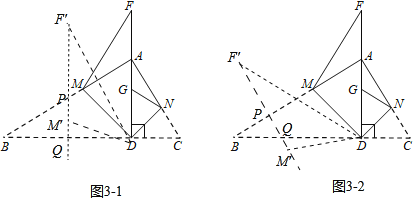
∴∠F′DQ=90°-28°=62°,
∵∠FDB=90°,
∴∠FDF′=90°-62°=28°,
∴旋转角为28°.
②如图3-2,当∠BPQ=90°时,
∵∠B=∠F′=28°,
∴∠PQB=90°-28°=62°,
∵∠PQB=∠F′+∠F′DB,
∴∠F′DB=62°-28°=34°,
∴∠FDF′=90°-34°=56°,
∴旋转角为56°,
同法可得当旋转角为208°或236°时,也满足条件,
综上所述,满足条件的旋转角为28°或56°或208°或236°.