题目内容
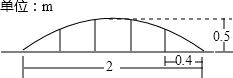某公园草坪的防护栏是由150段形状相同的抛物线组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（ ）分析：建立坐标系，可设解析式为y=ax2+0.5，结合图象求得解析式；再根据对称性求得不锈钢支柱的长度后，再求出总长度即可．
解答：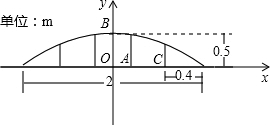
解：建立平面直角坐标系，可设抛物线解析式为y=ax2+0.5，
∵（1，0）在抛物线上，
∴a+0.5=0，
解得a=-0.5，
∴y=-0.5x2+0.5，
当x=0.2时y=0.48，
当x=0.6时y=0.32，
∴一段防护栏需要不锈钢支柱的总长=2×（0.48+0.32）=1.6米，
∴所需不锈钢管的总长度为：1.6×150=240米．
故选A．
解：建立平面直角坐标系，可设抛物线解析式为y=ax2+0.5，∵（1，0）在抛物线上，
∴a+0.5=0，
解得a=-0.5，
∴y=-0.5x2+0.5，
当x=0.2时y=0.48，
当x=0.6时y=0.32，
∴一段防护栏需要不锈钢支柱的总长=2×（0.48+0.32）=1.6米，
∴所需不锈钢管的总长度为：1.6×150=240米．
故选A．
点评：考查了二次函数的应用，建立恰当的坐标系是解决本题的突破点．
练习册系列答案
阅读快车系列答案
相关题目
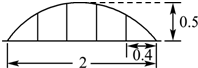某公园草坪的防护栏是由100段形状相同的抛物线形组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为（ ）
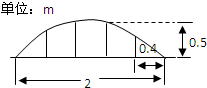某公园草坪的防护栏是由100段形状相同的抛物线形组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏需要不锈钢支柱的总长度至少为
某公园草坪的防护栏是由100段形状相同的抛物线组成的．为了牢固起见，每段护栏需要间距0.4m加设一根不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则这条防护栏的不锈钢支柱AB的长度为（ ）