题目内容
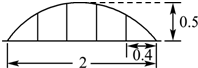 某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )分析:建立如图所示的直角坐标系,根据题意得到A点坐标为(-1,0)、B点坐标为((1,0),C点坐标为(0,0.5),D点坐标为(0.2,0),F点坐标为(0.6,0),然后利用待定系数法求出二次函数的解析式:设二次函数的交点式y=a(x-1)(x+1),把C(0,0.5)代入得a=-0.5,则抛物线解析式为y=-0.5x2+0.5,然后分别把x=0.2,x=0.6代入可得到DE=0.48,FP=0.32,于是可计算出每段护栏需要不锈钢支柱的长度,再把结果乘以100即可得到答案.
解答:解: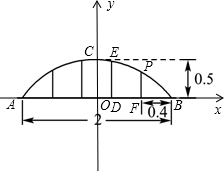 建立如图所示的直角坐标系,则A点坐标为(-1,0)、B点坐标为((1,0),C点坐标为(0,0.5),D点坐标为(0.2,0),F点坐标为(0.6,0),
建立如图所示的直角坐标系,则A点坐标为(-1,0)、B点坐标为((1,0),C点坐标为(0,0.5),D点坐标为(0.2,0),F点坐标为(0.6,0),
设抛物线解析式为y=a(x-1)(x+1),把C(0,0.5)代入得a=-0.5,
所以抛物线解析式为y=-0.5x2+0.5,
当x=0.2时,y=-0.5×0.22+0.5=0.48,
当x=0.6时,y=-0.5×0.62+0.5=0.32,
所以DE=0.48,FP=0.32,
所以每段护栏需要不锈钢支柱的长度=2(DE+FP)=2×(0.48+0.32)=1.6(m),
所以100段护栏需要不锈钢支柱的总长度=100×1.6m=160m.
故选C.
 建立如图所示的直角坐标系,则A点坐标为(-1,0)、B点坐标为((1,0),C点坐标为(0,0.5),D点坐标为(0.2,0),F点坐标为(0.6,0),
建立如图所示的直角坐标系,则A点坐标为(-1,0)、B点坐标为((1,0),C点坐标为(0,0.5),D点坐标为(0.2,0),F点坐标为(0.6,0),设抛物线解析式为y=a(x-1)(x+1),把C(0,0.5)代入得a=-0.5,
所以抛物线解析式为y=-0.5x2+0.5,
当x=0.2时,y=-0.5×0.22+0.5=0.48,
当x=0.6时,y=-0.5×0.62+0.5=0.32,
所以DE=0.48,FP=0.32,
所以每段护栏需要不锈钢支柱的长度=2(DE+FP)=2×(0.48+0.32)=1.6(m),
所以100段护栏需要不锈钢支柱的总长度=100×1.6m=160m.
故选C.
点评:本题考查了二次函数的应用:先建立适当的平面直角坐标系,然后把实际问题中的数据转化坐标系中的线段长或点的坐标,利用待定系数法求出二次函数的解析式,再利用二次函数的性质解决实际问题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
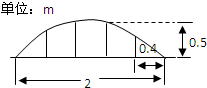 某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为
某公园草坪的防护栏是由100段形状相同的抛物线形组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为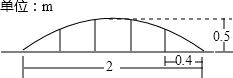 某公园草坪的防护栏是由150段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
某公园草坪的防护栏是由150段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( ) 某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏的不锈钢支柱AB的长度为( )
某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏的不锈钢支柱AB的长度为( )