题目内容
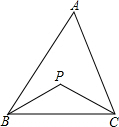
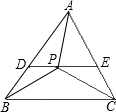 已知P是△ABC内任意一点(如图).
已知P是△ABC内任意一点(如图).(1)求证:
| 1 | 2 |
(2)若△ABC为正三角形,且边长为1,求证:PA+PB+PC<2.
分析:(1)由三角形两边之和大于第三边得PA+PB>c,PB+PC>a,PC+PA>b,则有PA+PB+PC>
(a+b+c);由定理4可知PA+PB<a+b,PB+PC<b+c,PC+PA<c+a,则有PA+PB+PC<a+b+c.从而得以证明.
(2)过P作DE∥BC交正三角形ABC的边AB,AC于D,E,可得PA<max{AD,AE}=AD,PB<BD+DP,PC<PE+EC,根据不等式的性质即可证明PA+PB+PC<2.
| 1 |
| 2 |
(2)过P作DE∥BC交正三角形ABC的边AB,AC于D,E,可得PA<max{AD,AE}=AD,PB<BD+DP,PC<PE+EC,根据不等式的性质即可证明PA+PB+PC<2.
解答:证明:(1)由三角形两边之和大于第三边得
PA+PB>c,PB+PC>a,PC+PA>b.把这三个不等式相加,再两边除以2,便得
PA+PB+PC>
(a+b+c).
又由定理4可知
PA+PB<a+b,PB+PC<b+c,
PC+PA<c+a.
把它们相加,再除以2,便得
PA+PB+PC<a+b+c.
所以
(a+b+c)<PA+PB+PC<a+b+c;
(2)过P作DE∥BC交正三角形ABC的边AB,AC于D,E,如图所示.于是
PA<max{AD,AE}=AD,
PB<BD+DP,PC<PE+EC,
所以PA+PB+PC<AD+BD+DP+PE+EC=AB+AE+EC=2.
PA+PB>c,PB+PC>a,PC+PA>b.把这三个不等式相加,再两边除以2,便得
PA+PB+PC>
| 1 |
| 2 |
又由定理4可知
PA+PB<a+b,PB+PC<b+c,
PC+PA<c+a.
把它们相加,再除以2,便得
PA+PB+PC<a+b+c.
所以
| 1 |
| 2 |
(2)过P作DE∥BC交正三角形ABC的边AB,AC于D,E,如图所示.于是
PA<max{AD,AE}=AD,
PB<BD+DP,PC<PE+EC,
所以PA+PB+PC<AD+BD+DP+PE+EC=AB+AE+EC=2.
点评:本题考查了三角形三边关系和正三角形的性质,同时考查了不等式的性质,综合性较强,有一定的难度.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
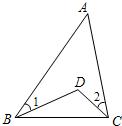
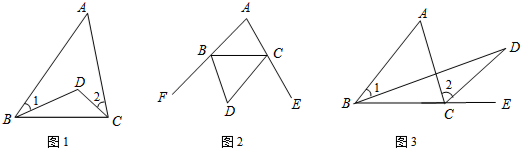
 已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.