题目内容
(25分)已知G是△ABC内任一点,BG、CG分别交AC、AB于点E、F.求使不等式S△BGF·S△CGE≤kS2△ABC恒成立的k的最小值.
 .从而,u2+(t-2)u+2t=0在[0,2]内有实根,则Δ=(t-2)2-8t≥0
.从而,u2+(t-2)u+2t=0在[0,2]内有实根,则Δ=(t-2)2-8t≥0t≥6+4
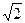 或t≤6-4
或t≤6-4 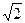 .
.从而t≤6-4 2.
所以,tmax="6-4"
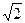 ,此时u="2"
,此时u="2" 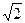 -2.
-2.因此,当u="2"
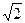 -2,x=y,即x=y=
-2,x=y,即x=y=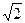 -1时,
-1时,(S△BFG·S△CEG/S2△ABC)max=
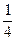 (6-4
(6-4 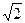 )2="17-12"
)2="17-12" 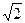 .
.故k≥17-12
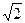 ,kmin="17-12"
,kmin="17-12" 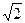 .解析:
.解析:略

练习册系列答案
相关题目
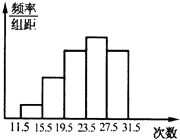 的频数是25,根据已知条件回答下列问题:
的频数是25,根据已知条件回答下列问题: