��Ŀ����
��֪��ABC��
��1����ͼ1����D���ǡ�ABC����һ�㣬BD��CD�ֱ�Ϊ��ABC����ACB�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��2����D���ǡ�ABC��һ�㣬λ����ͼ2��ʾ��BD��CD�ֱ�Ϊ��FBC����ECB�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��3����D���ǡ�ABC��һ�㣬λ����ͼ3��ʾ��BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��1����ͼ1����D���ǡ�ABC����һ�㣬BD��CD�ֱ�Ϊ��ABC����ACB�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��D=90��+
��A
| 1 |
| 2 |
��D=90��+
��A
��| 1 |
| 2 |
��2����D���ǡ�ABC��һ�㣬λ����ͼ2��ʾ��BD��CD�ֱ�Ϊ��FBC����ECB�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��D=90��-
��A
| 1 |
| 2 |
��D=90��-
��A
��| 1 |
| 2 |
��3����D���ǡ�ABC��һ�㣬λ����ͼ3��ʾ��BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���ߣ� ���D����A�Ĺ�ϵΪ
��D=
��A
| 1 |
| 2 |
��D=
��A
��| 1 |
| 2 |

��������1���ȸ��ݽ�ƽ���ߵ����������DBC����DCB���A�Ĺ�ϵ���ٸ����������ڽǺͶ�����⼴�ɣ�
��2���ȸ���BD��CD�ֱ��ǡ�CBE����BCF��ƽ���߿�֪��DBC=
��EBC����BCD=
��BCF�����ɡ�CBE����BCF�ǡ�ABC��������ǵó���CBE+��BCF=360��-��180��-��A��=180��+��A���ʡ�DBC+��BCD=
����EBC+��BCD��=
��180��+��A��=90��+
��A�������ڡ�DBC�С�BDC=180��-����DBC+��BCD�����ɵó����ۣ�
��3���ȸ���BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���߿�֪��1=��DBC=
��ABC����2=��DCE�����ɡ�DCE�ǡ�BCD����ǵó���DCE=��D+��DBE���ٸ��ݡ�ACE�ǡ�ABC����Ǽ��ɵó���ACE=��A+��ABC�ɴ˼��ɵó����ۣ�
��2���ȸ���BD��CD�ֱ��ǡ�CBE����BCF��ƽ���߿�֪��DBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��3���ȸ���BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���߿�֪��1=��DBC=
| 1 |
| 2 |
����⣺��1������BD��CD�ǡ�ABC�͡�ACB�Ľ�ƽ���ߣ�
���DBC=
��ABC����DCB=
��ACB��
�ߡ�ABC+��ACB=180��-��A��
��BDC=180��-��DBC-��DCB=180��-
����ABC+��ACB��=180��-
��180��-��A��=90��+
��A��
���BDC=90��+
��A��
����D=90��+
��A��
��2������BD��CD�ֱ��ǡ�CBE����BCF��ƽ����
���DBC=
��EBC����BCD=
��BCF��
�ߡ�CBE����BCF�ǡ�ABC���������
���CBE+��BCF=360��-��180��-��A��=180��+��A
���DBC+��BCD=
����EBC+��BCD��=
��180��+��A��=90��+
��A��
�ڡ�DBC�С�BDC=180��-����DBC+��BCD��=180��-��90��+
��A��=90��-
��A������D=90��-
��A��
��3����BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���ߣ�
���1=��DBC=
��ABC����2=��DCE=
����A+��ABC����
�ߡ�ACE�ǡ�ABC����ǣ�
���ACE=��A+��ABC��
�ߡ�DCE�ǡ�BCD����ǣ�
���D=��DCE-��DBC
=��DCE-��1
=
��ACE-
��ABC
=
����A+��ABC��-
��ABC
=
��A��
�ʴ�Ϊ����D=90��+
��A����D=90��-
��A����D=
��A��
���DBC=
| 1 |
| 2 |
| 1 |
| 2 |
�ߡ�ABC+��ACB=180��-��A��
��BDC=180��-��DBC-��DCB=180��-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���BDC=90��+
| 1 |
| 2 |
����D=90��+
| 1 |
| 2 |
��2������BD��CD�ֱ��ǡ�CBE����BCF��ƽ����
���DBC=
| 1 |
| 2 |
| 1 |
| 2 |
�ߡ�CBE����BCF�ǡ�ABC���������
���CBE+��BCF=360��-��180��-��A��=180��+��A
���DBC+��BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�ڡ�DBC�С�BDC=180��-����DBC+��BCD��=180��-��90��+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��3����BD��CD�ֱ�Ϊ��ABC����ECA�Ľ�ƽ���ߣ�
���1=��DBC=
| 1 |
| 2 |
| 1 |
| 2 |
�ߡ�ACE�ǡ�ABC����ǣ�
���ACE=��A+��ABC��
�ߡ�DCE�ǡ�BCD����ǣ�
���D=��DCE-��DBC
=��DCE-��1
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
�ʴ�Ϊ����D=90��+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���������⿼�������������ǵ����ʼ��������ڽǺͶ�������֪�����ε���ǵ�����֮�����ڵ������ڽǵĺ��ǽ�����Ĺؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
��֪ABC����������a2+b2+c2-ab-bc-ac=0������������ε���״�ǣ�������
| A��ֱ�������� | B������������ | C������ֱ�������� | D���ȱ������� |
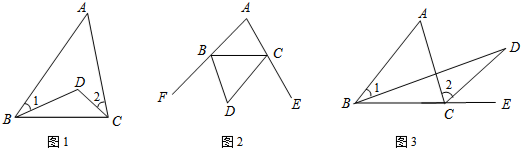
 ��ͼ����֪ABC�У�ADΪBC���ϵ����ߣ���AB=4cm��AC=3cm����AD��ȡֵ��Χ�ǣ�������
��ͼ����֪ABC�У�ADΪBC���ϵ����ߣ���AB=4cm��AC=3cm����AD��ȡֵ��Χ�ǣ�������| A��3��AD��4 | ||||
| B��1��AD��7 | ||||
C��
| ||||
D��
|
��֪��ABC�У�cosA=
��tgB=1�����ABC����״�ǣ�������
| 1 |
| 2 |
| A����������� |
| B��ֱ�������� |
| C���۽������� |
| D������������ |
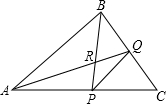 ��ͼ����֪��ABC����B��ƽ���߽���AC��P����A��ƽ���߽���BC��Q���������P��Q��C��ԲҲ����ABC������R����PQ=1����PR�ij�����
��ͼ����֪��ABC����B��ƽ���߽���AC��P����A��ƽ���߽���BC��Q���������P��Q��C��ԲҲ����ABC������R����PQ=1����PR�ij�����