题目内容
 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )分析:通过证明△ACB≌△ADB、△AEC≌∠AED,可以得到它们的对应边、对应角相等.从而证得△BCE≌△BDE.
解答: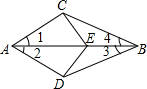 解:如图,在△ACB与△ADB中,
解:如图,在△ACB与△ADB中,
,则△ACB≌△ADB(SAS),所以BC=BD、∠3=∠4.故A、C选项正确;
如图,在△AEC与∠AED中,
,则△AEC≌∠AED(SAS),所以CE=DE.故B选项正确;
如图,在△BCE与△BDE中,
,则△BCE≌△BDE(SSS).
综上所述,图中共有三对全等三角形.故D选项错误;
故选:D.
 解:如图,在△ACB与△ADB中,
解:如图,在△ACB与△ADB中,
|
如图,在△AEC与∠AED中,
|
如图,在△BCE与△BDE中,
|
综上所述,图中共有三对全等三角形.故D选项错误;
故选:D.
点评:本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 15、如图,AB=BE,BC=BD,且BA平分∠CBE.
15、如图,AB=BE,BC=BD,且BA平分∠CBE. 如图,AC平分∠BAD,AB⊥BC,CA⊥CD,AC=CD,AB=3,则AD=
如图,AC平分∠BAD,AB⊥BC,CA⊥CD,AC=CD,AB=3,则AD= 如图,AD平分∠BAC,点F在BD上,FE∥AD交AB于G,交CA的延长线于E,试说明:∠AGE=∠E.
如图,AD平分∠BAC,点F在BD上,FE∥AD交AB于G,交CA的延长线于E,试说明:∠AGE=∠E. 如图,OP平分∠MON,点C为OP上的任意一点,CA⊥ON,垂足为A,线段OA的垂直平分线BG交OM于点B,交OA于点G,已知AB=6,AC=3,则△OBC的面积为
如图,OP平分∠MON,点C为OP上的任意一点,CA⊥ON,垂足为A,线段OA的垂直平分线BG交OM于点B,交OA于点G,已知AB=6,AC=3,则△OBC的面积为