Question

【题目】在中，，将绕点顺时针旋转至，点的对应点分别是，连接线段与线段交于点M，连接．

（1）如图1，求证：；

（2）如图1，求证：OM平分；

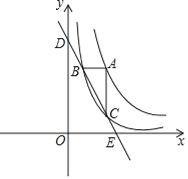
（3）如图2，若，求的长．

Answer 1

【答案】（1）见详解；（2）见详解；（3）

【解析】

（1）根据旋转的性质及OA＝OB可得OA＝OC＝OB＝OD，∠AOC＝∠BOD，然后根据“SAS”证明△AOC≌△BOD即可得证；

（2）过点O作OE⊥AC，OF⊥BD，利用等积法可得OE＝OF，再根据“HL”可证得Rt△MOE≌Rt△MOF即可得证；

（3）过点M作MH⊥AO，由可得∠OAC＝∠ODB＝45°，进而可证得△AOM≌△DOM，则∠MOD＝∠MOA，利用及 可得∠MOA＝60°，设OH＝x，利用30°、45°的直角三角形的性质及勾股定理可表示出MO、MH、AH、AM的长，根据列出方程求解，进而可求得CM的长．

（1）证明：∵旋转，

∴OA＝OC，OB＝OD，∠AOC＝∠BOD，

∵OA＝OB，

∴OA＝OC＝OB＝OD，

在△AOC与△BOD中，

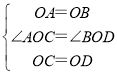
∴△AOC≌△BOD（SAS），

∴AC＝BD；

（2）证明：过点O作OE⊥AC，OF⊥BD，垂足分别为E、F，

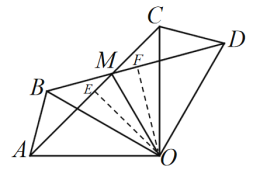
∵△AOC≌△BOD，

∴S△AOC＝S△BOD，

∵OE⊥AC，OF⊥BD，

∴，

∵AC＝BD，

∴OE＝OF，

∵OE⊥AC，OF⊥BD，

∴∠MEO＝∠MFO＝90°，

在Rt△MOE与Rt△MOF中，

∴Rt△MOE≌Rt△MOF（HL），

∴∠OME＝∠OMF，

∴OM平分；

（3）解：过点M作MH⊥AO，垂足为点H，

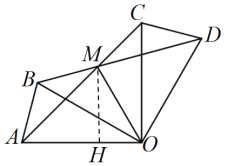
∵，OA＝OC，OB＝OD，

∴∠OAC＝∠ODB＝45°，

在△AOM与△DOM中，

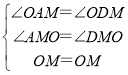
∴△AOM与△DOM（AAS），

∴∠AOM ＝∠DOM，

∵∠BOD＝，∠AOB＝30°，

∴∠AOM ＝∠DOM＝60°，

∵MH⊥AO，

∴∠MHO＝∠MHA＝90°，

∴在Rt△MHO中，∠OMH＝30°，

设OH＝x，则MO＝2OH＝2x，

∴，

∴在Rt△MHA中，∠HAM＝45°，

∴AH＝MH＝，

∴，

∵,

∴

解得：x＝2，

∴，

在Rt△AOC中，，

∴，

∴CM的长为．