ЬтФПФкШн
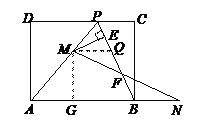
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮABCDЕФвЛЬѕБпAD=8 cmЃЌЕуPдкCDБпЩЯЃЌAP=ABЃЌ PC=4cmЃЌСЌНсPBЃЎЕуMДгЕуPГіЗЂЃЌбиPAЗНЯђдШЫйдЫЖЏЃЈЕуMгыЕуPЁЂAВЛжиКЯЃЉЃЛЕуNЭЌЪБДгЕуBГіЗЂЃЌбиЯпЖЮABЕФбгГЄЯпдШЫйдЫЖЏЃЌСЌНсMNНЛPBгкЕуFЃЎ
ЃЈ1ЃЉЧѓABЕФГЄЃЛ
ЃЈ2ЃЉШєЕуMЕФдЫЖЏЫйЖШЮЊ1cm/sЃЌЕуNЕФдЫЖЏЫйЖШЮЊ2cm/sЃЌЁїAMNЕФУцЛ§ЮЊSЃЌЕуMКЭЕуNЕФдЫЖЏЪБМфЮЊ![]() ЃЌЧѓSгы
ЃЌЧѓSгы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓSЕФзюДѓжЕЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШєЕуMКЭЕуNЕФдЫЖЏЫйЖШЯрЕШЃЌзїMEЁЭBPгкЕуEЃЎЪдЮЪЕБЕуMЁЂNдкдЫЖЏЙ§ГЬжаЃЌЯпЖЮEFЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃПШєБфЛЏЃЌЫЕУїРэгЩЃЛШєВЛБфЃЌЧѓГіЯпЖЮEFЕФГЄЖШЃЎ
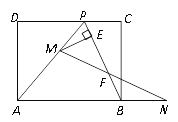
ЁОД№АИЁПЃЈ1ЃЉ10ЃЛЃЈ2ЃЉ![]() ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЎЃЈ3ЃЉЕуMЁЂNдкдЫЖЏЙ§ГЬжаЃЌЯпЖЮEFЕФГЄЖШВЛБфЃЌГЄЖШЮЊ
ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЎЃЈ3ЃЉЕуMЁЂNдкдЫЖЏЙ§ГЬжаЃЌЯпЖЮEFЕФГЄЖШВЛБфЃЌГЄЖШЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшAB=xЃЌИљОнелЕўПЩЕУAP=CD=xЃЌDP=CD-CP=x-4ЃЌРћгУЙДЙЩЖЈРэЃЌдкRtЁїADPжаЃЌAD2+DP2=AP2ЃЌМД82+ЃЈx-4ЃЉ2=x2ЃЌМДПЩНтД№ЃЛЃЈ2ЃЉЙ§ЕуMзїMGЁЭANгкЕуGЃЌдђЁЯAGM=ЁЯDЃН90ЁуЃЌЫљвдЁЯAPD=ЁЯMAGЃЌдђRtЁїAPDЁзRtЁїMAGЃЌЫљвд![]() ЃЌМД
ЃЌМД![]() ЃЌПЩЕУГі
ЃЌПЩЕУГі![]() ЃЌ гжвђЮЊ
ЃЌ гжвђЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]()
![]()
![]() ЃЌдђЕБ
ЃЌдђЕБ![]() ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЛЃЈ3ЃЉзїMQЁЮANЃЌНЛPBгкЕуQЃЌЧѓГіMP=MQЃЌBN=QMЃЌЕУГіMP=MQЃЌИљОнMHЁЭPQЃЌЕУГіHQ=
ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЛЃЈ3ЃЉзїMQЁЮANЃЌНЛPBгкЕуQЃЌЧѓГіMP=MQЃЌBN=QMЃЌЕУГіMP=MQЃЌИљОнMHЁЭPQЃЌЕУГіHQ=![]() PQЃЌИљОнЁЯQMF=ЁЯBNFЃЌжЄГіЁїMFQЁеЁїNFBЃЌЕУГіQF=
PQЃЌИљОнЁЯQMF=ЁЯBNFЃЌжЄГіЁїMFQЁеЁїNFBЃЌЕУГіQF=![]() QBЃЌдйЧѓГіEF=
QBЃЌдйЧѓГіEF=![]() PBЃЌзюКѓДњШыHF=
PBЃЌзюКѓДњШыHF=![]() PBМДПЩЕУГіЯпЖЮEFЕФГЄЖШВЛБфЃЛ
PBМДПЩЕУГіЯпЖЮEFЕФГЄЖШВЛБфЃЛ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЩшAB= ![]() ЃЌдђAP=
ЃЌдђAP= ![]() ЃЌDP=
ЃЌDP= ![]() ЃЌ
ЃЌ
дкRtЁїADPжаЃЌ гЩЙДЙЩЖЈРэЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК ![]() ЃЌ
ЃЌ
ЁрAB =10ЃЎ
ЃЈ2ЃЉЙ§ЕуMзїMGЁЭANгкЕуGЃЌдђЁЯAGM=ЁЯDЃН90ЁуЃЌ
ЁпDCЁЮABЃЌ
ЁрЁЯAPD=ЁЯMAGЃЌ
ЁрRtЁїAPDЁзRtЁїMAGЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]()
![]()
![]()
ЁрЕБ![]() ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЎ
ЪБЃЌSШЁЕУзюДѓжЕЮЊ45ЃЎ
ЃЈ3ЃЉзїMQЁЮANЃЌНЛPBгкЕуQЃЌ
ЁпAP=ABЃЌMQЁЮANЃЌ
ЁрЁЯAPB=ЁЯABPЃЌЁЯABP=ЁЯMQPЃЌ
ЁрЁЯAPB=ЁЯMQPЃЌ
ЁрMP=MQЃЌ
ЁпMEЁЭPQЃЌ
ЁрPE=EQ=![]() PQЃЌ
PQЃЌ
ЁпBN=PMЃЌPM=MQЃЌ
ЁрBN=QMЃЌ
ЁпMQЁЮANЃЌЁрЁЯQMF=ЁЯBNFЃЌ
дкЁїMFQКЭЁїNFBжаЃЌ
Ёп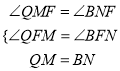 ЃЌ
ЃЌ
ЁрЁїMFQЁеЁїNFBЃЌ
ЁрQF=BFЃЌ
ЁрQF=![]() QBЃЌ
QBЃЌ
ЁрEF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PBЃЌ
PBЃЌ
дкRtЁїPBCжаЃЌ
ЁпPC=4ЃЌBC=8ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрEF=![]() PB=
PB=![]() ЃЌ
ЃЌ
ЁрЕуMЁЂNдкдЫЖЏЙ§ГЬжаЃЌЯпЖЮEFЕФГЄЖШВЛБфЃЌГЄЖШЮЊ![]() ЃЎ
ЃЎ