ĢāÄæÄŚČŻ
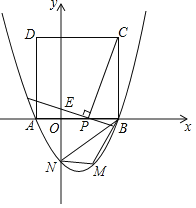
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµxOyÖŠ£¬¾ŲŠĪOABCµÄ¶„µćA”¢C·Ö±šŌŚxÖįŗĶyÖįÕż°ėÖįÉĻ£¬µćBµÄ×ų±źŹĒ£Ø5£¬2£©£¬µćPŹĒCB±ßÉĻŅ»¶Æµć£Ø²»ÓėµćC”¢µćBÖŲŗĻ£©£¬Į¬½įOP”¢AP£¬¹żµćO×÷ÉäĻßOE½»APµÄŃÓ³¤ĻßÓŚµćE£¬½»CB±ßÓŚµćM£¬ĒŅ”ĻAOP=”ĻCOM£¬ĮīCP=x£¬MP=y£®
£Ø1£©ĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öxµÄȔֵ·¶Ī§£»
£Ø2£©µ±xĪŖŗĪÖµŹ±£¬OP”ĶAP£æ
£Ø3£©ŌŚµćPµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚx£¬Ź¹”÷OCMµÄĆ껿Óė”÷ABPµÄĆ껿֮ŗĶµČÓŚ”÷EMPµÄĆ껿£æČō“ęŌŚ£¬ĒėĒóxµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
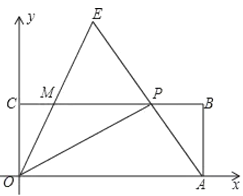
”¾“š°ø”æ£Ø1£©![]() (
(![]() )£»£Ø2£©µ±
)£»£Ø2£©µ±![]() Ź±£¬
Ź±£¬![]() £»£Ø3£©“ęŌŚ£¬
£»£Ø3£©“ęŌŚ£¬![]()
”¾½āĪö”æ
£Ø1£©Ö¤Ć÷![]() £¬µĆµ½
£¬µĆµ½![]() £¬µĆµ½x”¢yµÄŗÆŹż¹ŲĻµŹ½£¬
£¬µĆµ½x”¢yµÄŗÆŹż¹ŲĻµŹ½£¬
£Ø2£©ČōOP”ĶAP£¬ŌņæÉÖ¤µĆ![]() £¬µĆµ½¹ŲÓŚxµÄ·½³Ģ£¬½ā·½³Ģ£¬°Ń²»ŗĻĢāŅāÖµÉįČ„¼“æÉ£»
£¬µĆµ½¹ŲÓŚxµÄ·½³Ģ£¬½ā·½³Ģ£¬°Ń²»ŗĻĢāŅāÖµÉįČ„¼“æÉ£»
£Ø3£©¹żE×÷![]() ÓŚµćD£¬½»MPÓŚµćF£¬Ö¤Ć÷
ÓŚµćD£¬½»MPÓŚµćF£¬Ö¤Ć÷![]() £¬µĆµ½¹ŲÓŚyµÄ·½³Ģ£¬Ēó³öy£¬ŌŚøł¾Ż£Ø1£©Ēó³öx£¬°Ń²»ŗĻĢāŅāÖµÉįČ„¼“æÉ£®
£¬µĆµ½¹ŲÓŚyµÄ·½³Ģ£¬Ēó³öy£¬ŌŚøł¾Ż£Ø1£©Ēó³öx£¬°Ń²»ŗĻĢāŅāÖµÉįČ„¼“æÉ£®
£Ø1£©ČēĶ¼£¬”ßBC”ĪOA£¬
”ą![]() £®
£®
”ß![]() £¬
£¬
”ą![]() £®
£®
”ß![]() £¬
£¬
”ą![]() £®
£®
”ą![]() £¬¼“
£¬¼“![]() £®
£®
”ą![]() £¬xµÄȔֵ·¶Ī§ŹĒ
£¬xµÄȔֵ·¶Ī§ŹĒ![]() £®
£®
£Ø2£©ČēĶ¼£¬ÓÉĢāŅāÖŖ£¬
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬”ą
£¬”ą![]() £®
£®
”ą![]() £®”ą
£®”ą![]() £®
£®
”ą![]() £¬¼“
£¬¼“![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬![]() £Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£®
”ąµ±![]() Ź±£¬
Ź±£¬![]() £®
£®
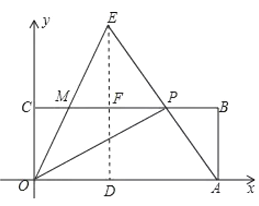
£Ø3£©¼ŁÉč“ęŌŚx·ūŗĻĢāŅā£®
ČēĶ¼£¬¹żE×÷![]() ÓŚµćD£¬½»MPÓŚµćF£¬Ōņ
ÓŚµćD£¬½»MPÓŚµćF£¬Ōņ![]() £®
£®
”ß![]() Óė
Óė![]() Ć껿֮ŗĶµČÓŚ
Ć껿֮ŗĶµČÓŚ![]() µÄĆ껿£¬
µÄĆ껿£¬
”ą![]() £®
£®
”ą![]() £¬
£¬![]() £®
£®
”ßPM”ĪOA£¬
”ą![]() £®
£®
”ą![]() £®
£®
¼“![]() £¬½āµĆ
£¬½āµĆ![]() £®
£®
”ąÓÉ£Ø2£©![]() µĆ£¬
µĆ£¬![]() £®
£®
½āµĆ![]() £¬
£¬![]() £¬£Ø²»ŗĻĢāŅāÉįČ„£©£®
£¬£Ø²»ŗĻĢāŅāÉįČ„£©£®
”ąŌŚµćPµÄŌĖ¶Æ¹ż³ĢÖŠ£¬“ęŌŚ![]() £¬Ź¹
£¬Ź¹![]() Óė
Óė![]() Ć껿֮ŗĶµČÓŚ
Ć껿֮ŗĶµČÓŚ![]() µÄĆ껿£®
µÄĆ껿£®