题目内容
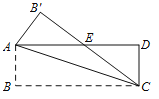
【题目】如图，矩形ABCD中，AB＝2 cm，BC＝6cm，把△ABC沿对角线AC折叠，得到△AB’C，且B’C与AD相交于点E，则AE的长为___cm．
【答案】
【解析】先根据等角对等边，得出AE=CE，再设AE=CE=x，在Rt△CDE中，根据勾股定理列出关于x的方程，求得x的值即可．
解：由折叠得，∠BCA=∠ACB′，
由AD∥BC得，∠BCA=∠CAD，
∴∠ACB′=∠CAD，
∴AE=CE，
设AE=CE=x，则DE=6–x，
在Rt△CDE中，DE2+CD2=CE2，即（6–x）2+22=x2，
解得x=，
∴AE的长为cm．
故答案为：．
“点睛”本题以折叠问题为背景，主要考查了轴对称的先行者以及勾股定理，折叠是一种对称变换，它属于轴对称，折叠前后的对应边和对应角相等. 解题时，我们常设所求的线段长为x，然后用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解.
练习册系列答案
相关题目
