题目内容
【题目】如图,在△ABC中,AB=AC,点M在△ABC内,AM平分∠BAC.点D与点M在AC所在直线的两侧,AD⊥AB,AD=BC,点E在AC边上,CE=AM,连接MD、BE.
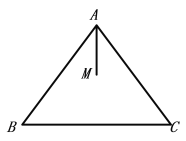
(1)补全图形;
(2)请判断MD与BE的数量关系,并进行证明;
(3)点M在何处时,BM+BE会有最小值,画出图形确定点M的位置;如果AB=5,BC=6,求出BM+BE的最小值.
【答案】(1)作图见解析(2)MD=BE,证明见解析(3)作图见解析, BM+BE的最小值为![]()
【解析】
(1)根据题意补全图形即可;
(2)利用SAS即可证明△EAB≌△DAC,可得结论:BE=CD;
(3)当点M在BD上时,根据两点之间线段最短,即可得到BM+BE会有最小值,最小值为BD.
(1)补全图形如图
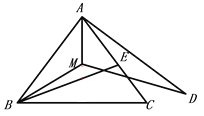
(2)MD=BE
证明:延长AM交BC于点F(如图2).
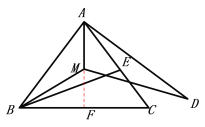
∵AM平分∠BAC,
∴∠BAM=∠CAM.
∵AD⊥AB,
∴∠MAD+∠BAM=90°.
∴∠MAD+∠CAM=90°
∵AB=AC,AM平分∠BAC,
∴AF⊥BC.
∴∠C+∠CAM=90°.
∴∠MAD=∠C.
又∵AM=CE,AD=BC,
∴△AMD≌△CEB.
∴MD=BE.
(3)点M的位置如图
∵AB=5,BC=6,
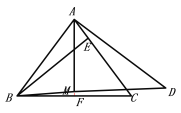
∴AD=BC=6,.
∴![]()
∴BM+BE的最小值为![]() .
.

练习册系列答案
相关题目