题目内容
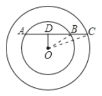
【题目】如图，以O为圆心的两个同心圆中，小圆的弦AB的延长线交大圆于点C，若AB=3，BC=1，则与圆环的面积最接近的整数是（ ）
A. 9 B. 10 C. 15 D. 13
【答案】D
【解析】
过O作OD⊥AC交AC于D，连接OB、OC，利用垂径定理求出BD的值，再根据勾股定理和圆环的面积公式计算.
过O作OD⊥AC交AC于D，连接OB、OC，如图，
根据垂径定理得BD＝
×AB＝
＝1.5，CD＝BD＋BC＝
＝2.5，∵OB2＝OD2＋BD2，OC2＝OD2＋CD2，根据圆环面积公式得：圆环面积＝π×OC2－π×OB2＝π×（OC2－ OB2）＝π×（CD2－ BD2）＝π×（2.52－1.52）＝4π≈12.56，故答案选D.
练习册系列答案
相关题目
