题目内容
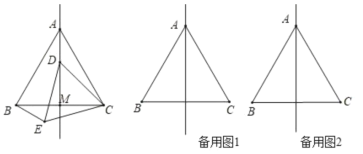
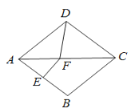
【题目】如图,在菱形ABCD中, 边AB的垂直平分线交对角线AC于点F,垂足为点E,连结DF,若∠BAD=80°,则∠CDF的度数为( )
A.80°B.70°C.65°D.60°
【答案】D
【解析】
根据菱形的四条边都相等可得AB=AD,对边平行可得AB∥CD,再根据两直线平行,同旁内角互补求出∠ADC,根据菱形的对角线平分一组对角线可得∠BAF=∠DAF,根据线段垂直平分线上的点到两端点的距离相等可得AF=BF,根据等边对等角可得∠BAF=∠ABF,再利用“边角边”证明△ABF和△ADF全等,根据全等三角形对应角相等可得∠ADF=∠ABF,然后根据∠CDF=∠ADC-∠ADF代入数据计算即可得解.
如图,连接FB
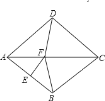
∵四边形ABCD是菱形,
∴AB=AD,AB∥CD,
∴∠ADC=180°-∠BAD=180°-80°=100°,
在菱形ABCD中,∠BAF=∠DAF=![]() ∠BAD=
∠BAD=![]() ×80°=40°,
×80°=40°,
∵EF垂直平分AB,
∴AF=BF,
∴∠BAF=∠ABF=40°,
在△ABF和△ADF中,
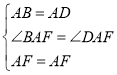
∴△ABF≌△ADF(SAS),
∴∠ADF=∠ABF=40°,
∴∠CDF=∠ADC-∠ADF,
=100°-40°,
=60°.
故选D.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目