题目内容
【题目】已知，等腰
中，
，
是高
上任一点，
是腰
上任一点，腰
，
，
，那么线段
的最小值是____________.
【答案】
【解析】
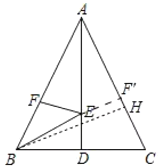
如图作等F关于AD的对称点F′，连接EF′．作BH⊥AC于H．根据垂线段最短可知，当B，E，F′共线，即F′与H重合时，BE＋EF的值最小，最小值就是线段BH的长，然后求出BH即可．
解：如图，作点F关于AD的对称点F′，连接EF′，作BH⊥AC于H．
∵AB＝AC，AD⊥BC，
∴BD＝CD＝3，
∴点F′在AC上，
∵BE＋EF＝BE＋EF′，
根据垂线段最短可知，当B，E，F′共线，即F′与H重合时，BE＋EF的值最小，最小值就是线段BH的长．
在Rt△ACD中，AC＝5，
∵
BCAD＝ACBH，
∴BH＝
，
∴BE＋EF的最小值为，
故答案为:．
练习册系列答案
相关题目
