题目内容
在- 次数学活动课上,老师出了- 道题:
(1) 解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法( 分解因式法) 。
接着, 老师请大家用自己熟悉的方法解第二道题:
(2) 解关于x 的方程mx2+(m -3)x -3=0(m 为常数,且m ≠0).
老师继续巡视,及时观察、点拨大家. 再接着, 老师将第二道题变式为第三道题:
(3) 已知关于x 的函数y=mx2+(m-3)x-3(m 为常数).
①求证:不论m 为何值, 此函数的图象恒过x 轴、y 轴上的两个定点( 设x 轴上的定点为A ,y 轴上的定点为C) ;
②若m ≠0 时, 设此函数的图象与x 轴的另一个交点为反B, 当△ABC 为锐角三角形时, 求m 的取值范围;当△ABC 为钝角三角形时,观察图象,直接写出m 的取值范围.
请你也用自己熟悉的方法解上述三道题.

(1) 解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法( 分解因式法) 。
接着, 老师请大家用自己熟悉的方法解第二道题:
(2) 解关于x 的方程mx2+(m -3)x -3=0(m 为常数,且m ≠0).
老师继续巡视,及时观察、点拨大家. 再接着, 老师将第二道题变式为第三道题:
(3) 已知关于x 的函数y=mx2+(m-3)x-3(m 为常数).
①求证:不论m 为何值, 此函数的图象恒过x 轴、y 轴上的两个定点( 设x 轴上的定点为A ,y 轴上的定点为C) ;
②若m ≠0 时, 设此函数的图象与x 轴的另一个交点为反B, 当△ABC 为锐角三角形时, 求m 的取值范围;当△ABC 为钝角三角形时,观察图象,直接写出m 的取值范围.
请你也用自己熟悉的方法解上述三道题.

解:(1)由x2-2x-3=0,得(x+1)(x-3)=0
∴x1=1,x2=3
(2)方法一:由mx2+(m-3)x-3=0得(x+1)·(mx-3)=0
∵m≠0, ∴x1=-1,x2=
方法2:由公式法:
∴x1=-1,x2=
(3)①I: 当m=0时,函数y= mx2+(m-3)x-3为y=-3x-3,令y=0,得x=-1
令x=0,则y=-3.
∴直线y=-3x-3过定点A(-1,0),C(0,-3)
II: 当m≠0时,函数y= mx2+(m-3)x-3为y=(x+1)·(mx-3)
∴抛物线y=(x+1)·(mx-3)恒过两定点A(-1,0),C(0,-3)和B( ,0)
,0)
②当m>0时,由①可知抛物线开口向上,
且过点A(-1,0),C(0,-3)和B( ,0),
,0),
观察图象,可知,当⊿ABC为Rt⊿时,
则⊿AOC∽⊿COB
∴
∴
∴32=1×
∴x1=1,x2=3
(2)方法一:由mx2+(m-3)x-3=0得(x+1)·(mx-3)=0
∵m≠0, ∴x1=-1,x2=

方法2:由公式法:

∴x1=-1,x2=

(3)①I: 当m=0时,函数y= mx2+(m-3)x-3为y=-3x-3,令y=0,得x=-1
令x=0,则y=-3.
∴直线y=-3x-3过定点A(-1,0),C(0,-3)
II: 当m≠0时,函数y= mx2+(m-3)x-3为y=(x+1)·(mx-3)
∴抛物线y=(x+1)·(mx-3)恒过两定点A(-1,0),C(0,-3)和B(
 ,0)
,0)②当m>0时,由①可知抛物线开口向上,
且过点A(-1,0),C(0,-3)和B(
 ,0),
,0), 观察图象,可知,当⊿ABC为Rt⊿时,
则⊿AOC∽⊿COB
∴

∴

∴32=1×


练习册系列答案
相关题目
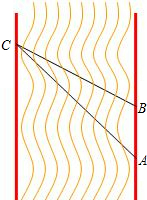 在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈

 在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上. 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.