题目内容
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.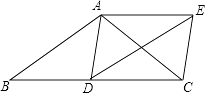
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
【答案】
(1)证明:∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
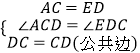 ,
,
∴△ADC≌△ECD(SAS);
(2)证明:∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴ADCE是矩形.
【解析】(1)由平行四边形的性质易得对边平行且相等,又由等边对等角,可得两个三角形有两组对边相等且夹角相等,可判定两个三角形全等。
(2)由四边形ABDE是平行四边形易得四边形ADCE是平行四边形,在利用等腰三角形的性质“三线合一”可得∠ADC=90°,最终可得ADCE是矩形.
【考点精析】关于本题考查的矩形的判定方法,需要了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目