题目内容
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,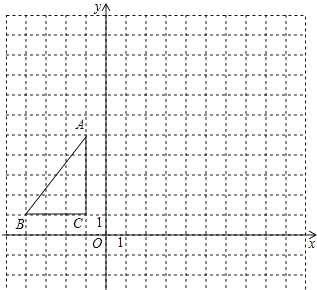
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
【答案】
(1)解:△AB′C′如图所示
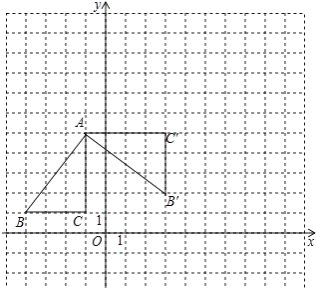
(2)解:点B′的坐标为(3,2),点C′的坐标为(3,5)
(3)解:点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,
∵AC=4,
∴弧长为: ![]() =
= ![]() =2π,
=2π,
即点C经过的路径长为2π.
【解析】(1)根据旋转的性质按要求画出△AB′C′。
(2)观察图形写出点B′,C′的坐标。
(3)根据旋转的现在可知点C经过的路径为以点A为圆心,圆心角为90°,AC为半径的圆弧,根据弧长公式求出弧CC′的长即可

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目