题目内容
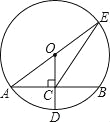
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
【答案】
【解析】
试题分析:由OD⊥AB,根据垂径定理得到AC=BC=![]() AB=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中根据勾股定理得到x2=42+(x﹣2)2,解得x=5,则AE=10,OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
AB=4,设AO=x,则OC=OD﹣CD=x﹣2,在Rt△ACO中根据勾股定理得到x2=42+(x﹣2)2,解得x=5,则AE=10,OC=3,再由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
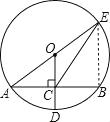
试题解析:连结BE,如图,
∵OD⊥AB,
∴AC=BC=![]() AB=
AB=![]() ×8=4,
×8=4,
设AO=x,则OC=OD﹣CD=x﹣2,
在Rt△ACO中,∵AO2=AC2+OC2,
∴x2=42+(x﹣2)2,解得 x=5,
∴AE=10,OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=![]() .
.

练习册系列答案
相关题目
【题目】如表是小明同学参加“一分钟汉字听写”训练近6次的成绩:
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
听写字数 | 245 | 248 | 240 | 243 | 246 | 242 |
则这组数据的平均数和中位数分别是( )
A. 245个、244个B. 244个、244个
C. 244个、241.5个D. 243个、244个