题目内容
【题目】如图，∠AOB=90°，OA=45cm，OB=15cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？
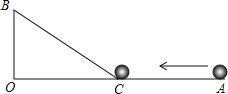
【答案】25cm.
【解析】
试题本题考查勾股定理的实际应用问题，结合了物理知识以及小球的动态变化，根据题意可以直到小球滚动的速度与机器人行走的速度相等，运动时间相等，得出BC=AC，由勾股定理可求得BC的长．
试题解析：∵小球滚动的速度与机器人行走的速度相等，运动时间相等，
即BC=CA，设AC为x，则OC=45-x， 由勾股定理可知OB2+OC2=BC2，
又∵OA=45，OB=15， 把它代入关系式152+（45-x）2=x2，
解方程得出x=25（cm）．
答：如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是25cm．
练习册系列答案
相关题目
