题目内容
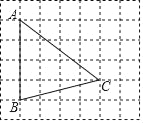
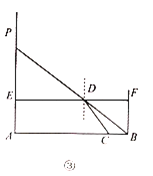
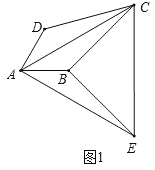
【题目】如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,将AC绕着点A顺时针旋转60°得AE,连接BE,CE.
(1)求证:△ADC≌△ABE;
(2)求证:![]()
(3)若AB=2,点Q在四边形ABCD内部运动,且满足![]() ,直接写出点Q运动路径的长度.
,直接写出点Q运动路径的长度.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)推出∠DAC=∠BAE,则可直接由SAS证明△ADC≌△ABE;
(2)证明△BCE是直角三角形,再证DC=BE,AC=CE即可推出结论;
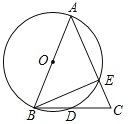
(3)如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,证△ADQ≌△ABF,由勾股定理的逆定理证∠FBQ=90°,求出∠DQB=150°,确定点Q的路径为过B,D,C三点的圆上![]() ,求出
,求出![]() 的长即可.
的长即可.
(1)证明:∵∠CAE=∠DAB=60°,
∴∠CAE-∠CAB=∠DAB-∠CAB,
∴∠DAC=∠BAE,
又∵AD=AB,AC=AE,
∴△ADC≌△ABE(SAS);
(2)证明:在四边形ABCD中,
∠ADC+∠ABC=360°-∠DAB-∠DCB=270°,
∵△ADC≌△ABE,
∴∠ADC=∠ABE,CD=BE,
∴∠ABC+ABE=∠ABC+∠ADC=270°,
∴∠CBE=360°-(∠ABC+ABE)=90°,
∴CE2=BE2+BC2,
又∵AC=AE,∠CAE=60°,
∴△ACE是等边三角形,
∴CE=AC=AE,
∴AC2=DC2+BC2;
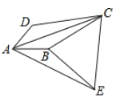
(3)解:如图2,设Q为满足条件的点,将AQ绕着点A顺时针旋转60度得AF,连接QF,BF,QB,DQ,AF,
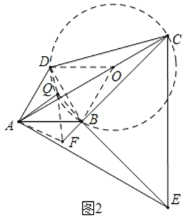
则∠DAQ=∠BAF,AQ=QF,△AQF为等边三角形,
又∵AD=AB,
∴△ADQ≌△ABF(SAS),
∴AQ=FQ,BF=DQ,
∵AQ2=BQ2+DQ2,
∴FQ2=BQ2+BF2,
∴∠FBQ=90°,
∴∠AFB+∠AQB=360°-(∠QAF+∠FBQ)=210°,
∴∠AQD+∠AQB=210°,
∴∠DQB=360°-(∠AQD+∠AQB)=150°,
∴点Q的路径为过B,D,C三点的圆上![]() ,
,
如图2,设圆心为O,则∠BOD=2∠DCB=60°,
连接DB,则△ODB与△ADB为等边三角形,
∴DO=DB=AB=2,
∴点Q运动的路径长为:![]() .
.