题目内容
【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PB、PA.
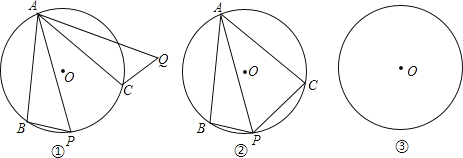
(Ⅰ)如图①,把△ABP绕点A逆时针旋转到△ACQ,求证:点P、C、Q三点在同一直线上.
(Ⅱ)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(Ⅲ)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.
【答案】(Ⅰ)见解析;(Ⅱ)PA=PC+CQ=PC+PB;(Ⅲ)PB+PC=2×![]() PA=
PA=![]() PA.
PA.
【解析】
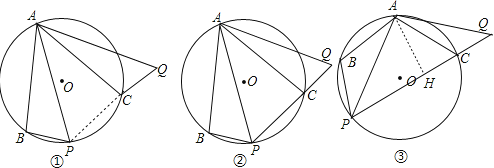
试题分析:(Ⅰ)连结PC,如图①,根据旋转的性质得∠ABP=∠ACQ,再根据圆内接四边形的性质得∠ABP+∠ACP=180°,则∠ACQ+∠ACP=180°,于是可判断点P、C、Q三点在同一直线上;
(Ⅱ)把△ABP绕点A逆时针旋转到△ACQ,如图②,则由①得点P、C、Q三点在同一直线上,根据旋转的性质得∠BAP=∠CAQ,AP=AQ,PB=CQ,而∠BAP+∠PAC=60°,则∠PAC+∠CAQ=60°,即∠PAQ=60°,于是可判断△APQ为等边三角形,所以PQ=PA=PB+PC;
(Ⅲ)把△ABP绕点A逆时针旋转到△ACQ,如图③,由①得点P、C、Q三点在同一直线上,∠BAP=∠CAQ,AP=AQ,PB=CQ,由∠BAP+∠PAC=120°,得到∠PAC+∠CAQ=120°,即∠PAQ=120°,可计算出∠P=∠Q=30°,作AH⊥PQ,根据等腰三角形的性质得PH=QH,在Rt△APH中,利用余弦的定义得cos∠APH=cos30°=![]() =
=![]() ,则PH=
,则PH=![]() PA,由于PQ=PC+CQ=PC+PB=2PH,所以得到PB+PC=
PA,由于PQ=PC+CQ=PC+PB=2PH,所以得到PB+PC=![]() PA.
PA.
(Ⅰ)证明:连结PC,如图①,
∵把△ABP绕点A逆时针旋转到△ACQ,
∴∠ABP=∠ACQ,
∵四边形ABPC为⊙O的内接四边形,
∴∠ABP+∠ACP=180°,
∴∠ACQ+∠ACP=180°,
∴点P、C、Q三点在同一直线上;
(Ⅱ)解:PA=PB+PC.理由如下:
把△ABP绕点A逆时针旋转到△ACQ,如图②,
由①得点P、C、Q三点在同一直线上,∠BAP=∠CAQ,AP=AQ,PB=CQ,
而∠BAC=60°,即∠BAP+∠PAC=60°,
∴∠PAC+∠CAQ=60°,即∠PAQ=60°,
∴△APQ为等边三角形,
∴PQ=PA,
∴PA=PC+CQ=PC+PB;
(Ⅲ)(2)中的结论不成立,PA、PB、PC之间的关系为![]() PA=PB+PC.理由如下:
PA=PB+PC.理由如下:
把△ABP绕点A逆时针旋转到△ACQ,如图③,
由①得点P、C、Q三点在同一直线上,∠BAP=∠CAQ,AP=AQ,PB=CQ,
而∠BAC=120°,即∠BAP+∠PAC=120°,
∴∠PAC+∠CAQ=120°,即∠PAQ=120°,
∴∠P=∠Q=30°,
作AH⊥PQ,则PH=QH,
在Rt△APH中,cos∠APH=cos30°=![]() =
=![]() ,
,
∴PH=![]() PA,
PA,
而PQ=PC+CQ=PC+PB=2PH,
∴PB+PC=2×![]() PA=
PA=![]() PA.
PA.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案