题目内容
观察下列方程和等式,寻找规律,完成问题:①方程x2-7x+6=0,x1=1,x2=6,而x2-7x+6=(x-1)(x-6);
②方程x2-4x-5=0,x1=5,x2=-1,而x2-4x-5=(x-5)(x+1);
③方程4x2-12x+9=0,x1=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
④方程3x2+7x+4=0,x1=-
| 4 |
| 3 |
| 4 |
| 3 |
(1)探究规律:当方程ax2+bx+c=0(a≠0)时,
(2)解决问题:根据上述材料将下列多项式分解:x2-x-2;2x2+3x-2
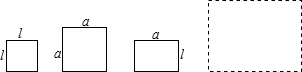
(3)拓广应用:已知,如图,现有1×1,a×a的正方形纸片和1×a的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为2a2+5a+2,并标出此矩形的长和宽.
分析:(1)求出一元二次方程的根即可进行因式分解;
(2)利用x2-x-2=0,根为x1=2,x2=-1,以及2x2+3x-2=0,得出x1=-2,x2=
,进而因式分解即可;
(3)根据2a2+5a+2=0,得出x1=-
,x2=-2,即可得出此矩形的长和宽.
(2)利用x2-x-2=0,根为x1=2,x2=-1,以及2x2+3x-2=0,得出x1=-2,x2=
| 1 |
| 2 |
(3)根据2a2+5a+2=0,得出x1=-
| 1 |
| 2 |
解答:解:(1)∵方程ax2+bx+c=0,
方程的根为:x=
,
∴ax2+bx+c=(x-
)(x-
);
(2)∵x2-x-2=0,
x1=2,x2=-1,
∴x2-x-2;
=(x-2)(x+1);
∵2x2+3x-2=0,
x1=-2,x2=
,
∴2x2+3x-2,
=(x+2)(2x-1);
(3)2a2+5a+2=0,
x1=-
,x2=-2,
∴2a2+5a+2,
=(2a+1)(a+2),
∴此矩形的长和宽分别为:2a+1,a+2.
方程的根为:x=
-b±
| ||
| 2a |
∴ax2+bx+c=(x-
-b+
| ||
| 2a |
-b-
| ||
| 2a |
(2)∵x2-x-2=0,
x1=2,x2=-1,
∴x2-x-2;
=(x-2)(x+1);
∵2x2+3x-2=0,
x1=-2,x2=
| 1 |
| 2 |
∴2x2+3x-2,
=(x+2)(2x-1);
(3)2a2+5a+2=0,
x1=-
| 1 |
| 2 |
∴2a2+5a+2,
=(2a+1)(a+2),
∴此矩形的长和宽分别为:2a+1,a+2.
点评:此题主要考查了因式分解的应用,根据已知得出求出方程的根是解题关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 ,
,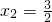 ,而
,而 ;
; ,x2=-1,而
,x2=-1,而 ;…
;…
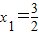 ,
,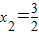 ,而
,而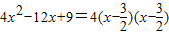 ;
;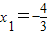 ,x2=-1,而
,x2=-1,而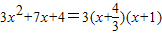 ;…
;…