题目内容
（2010•百色）如图，将边长为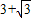
的等边△ABC折叠，折痕为DE，点B与点F重合，EF和DF分别交AC于点M、N，DF⊥AB，垂足为D，AD=1．设△DBE的面积为S，则重叠部分的面积为 ．（用含S的式子表示）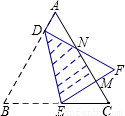
【答案】分析：阴影面积=△DBE的面积-S△NMF，根据翻折变换，△ADN≌△NMF，故能求出阴影面积．
解答：解：由题意可知，
∵△ABC 是等边三角形，
∴∠A=60°，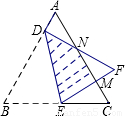
∵DF⊥AB，
∴∠ADN=90°，
∴∠AND=30°，
又AD=1，
∴AN=2，DN=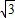
，DF=BD=2+
，
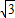∴NF=2，
∵∠AND=∠FNM，AN=NF，∠F=∠B=∠A=60°，
∴△ADN≌△NMF，
∴S△NMF=S△ADN，
∵DF⊥AB，
∴S△NMF=S△ADN=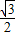
，
∵阴影面积=△DBE的面积-S△NMF，
∴阴影面积=S-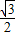
．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
解答：解：由题意可知，
∵△ABC 是等边三角形，
∴∠A=60°，
∵DF⊥AB，
∴∠ADN=90°，
∴∠AND=30°，
又AD=1，
∴AN=2，DN=
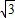，DF=BD=2+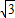，∴NF=2，
∵∠AND=∠FNM，AN=NF，∠F=∠B=∠A=60°，
∴△ADN≌△NMF，
∴S△NMF=S△ADN，
∵DF⊥AB，
∴S△NMF=S△ADN=
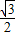，∵阴影面积=△DBE的面积-S△NMF，
∴阴影面积=S-
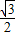．点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
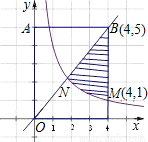
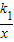（x＞0）与正比例函数y=k2x的图象分别交矩形OABC的BC边于M（4，1），B（4，5）两点．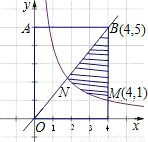
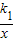（x＞0）与正比例函数y=k2x的图象分别交矩形OABC的BC边于M（4，1），B（4，5）两点．
