题目内容
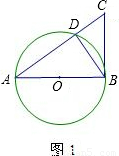
(2010•百色)如图1,AB是⊙O的直径,BC⊥AB,垂足为B,AC交⊙O于点D.(1)用尺规作图:过点D作DE⊥BC,垂足为E(保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,求证:△BED∽△DEC;
(3)若点D是AC的中点(如图2),求sin∠OCB的值.

【答案】分析:(1)根据过直线外一点作已知直线的垂线的方法进行求作;
(2)根据直径所对的圆周角是直角,得∠ADB=90°,则∠CDB=∠ADB=90°,再根据等角的余角相等,证明∠C=∠EDB,从而根据两角对应相等,就可证明三角形相似;
(3)在Rt△OBC中,只要找到OB与OC的关系即可.由于∠ADB=90°,D是AC的中点,所以BD垂直平分AC,则BC=AB=2OB;设OB=k,则BC=2k,根据勾股定理求得OC的长,从而求解.
解答:(1)解:如图,
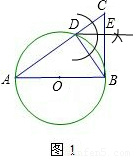
(2)证明:∵AB是⊙O的直径,
∴∠ADB=∠CDB=90°.
∴∠CDE+∠EDB=90°.
又∵DE⊥BC,
∴∠CED=∠DEB=90°,
∴∠CDE+∠C=90°.
∴∠C=∠EDB.
∴△BED∽△DEC.
(3)解:∵∠ADB=90°,D是AC的中点,
∴BD垂直平分AC.
∴BC=AB=2OB.
设OB=k,则BC=2k,
∴OC=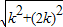 =
=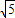 k.
k.
∴sin∠OCB=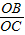 =
=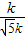 =
=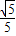 .
.
点评:此图综合考查了作垂线的方法、直径所对的圆周角是直角、相似三角形的判定、线段垂直平分线的性质、勾股定理以及锐角三角函数的求法.
(2)根据直径所对的圆周角是直角,得∠ADB=90°,则∠CDB=∠ADB=90°,再根据等角的余角相等,证明∠C=∠EDB,从而根据两角对应相等,就可证明三角形相似;
(3)在Rt△OBC中,只要找到OB与OC的关系即可.由于∠ADB=90°,D是AC的中点,所以BD垂直平分AC,则BC=AB=2OB;设OB=k,则BC=2k,根据勾股定理求得OC的长,从而求解.
解答:(1)解:如图,

(2)证明:∵AB是⊙O的直径,
∴∠ADB=∠CDB=90°.
∴∠CDE+∠EDB=90°.
又∵DE⊥BC,
∴∠CED=∠DEB=90°,
∴∠CDE+∠C=90°.
∴∠C=∠EDB.
∴△BED∽△DEC.
(3)解:∵∠ADB=90°,D是AC的中点,
∴BD垂直平分AC.
∴BC=AB=2OB.
设OB=k,则BC=2k,
∴OC=
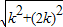 =
=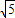 k.
k.∴sin∠OCB=
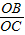 =
=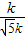 =
=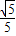 .
.点评:此图综合考查了作垂线的方法、直径所对的圆周角是直角、相似三角形的判定、线段垂直平分线的性质、勾股定理以及锐角三角函数的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
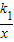 (x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
(x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.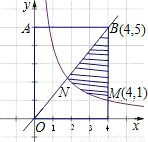
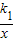 (x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
(x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.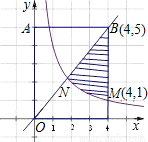
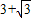 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1.设△DBE的面积为S,则重叠部分的面积为 .(用含S的式子表示)