题目内容
在平面直角坐标系中,抛物线y=x2+bx+c经过点(0,2)和点(2,2),点P为抛物线上一动点,如果直径为4的⊙P与坐标轴相切,那么满足条件的点P有______个.
- A.4个
- B.3个
- C.2个
- D.1个
B
分析:首先求得函数的解析式,根据点P为抛物线上一动点,直径为4的⊙P与坐标轴相切,得出圆心的横坐标为2或-2,求出即可.
解答:(1)∵抛物线y=x2+bx+c经过(0,2)和点(2,2),
∴将点代入解析式
解得:
抛物线的表达式为:y=x2-2x+2,
∵点P为抛物线上一动点,
当直径为4的⊙P与y轴相切,
∴圆心的横坐标为2或-2,
当x=2,y=x2-2x+2=4-4+2=2,
∴点P的坐标为:(2,2),
当x=-2,y=x2-2x+2=4+4+2=10,
∴点P的坐标为:(-2,10),
当直径为4的⊙P与y轴相切,
∴圆心的纵坐标为2
y=x2-2x+2=2
解得:x=2或0,
∴点P的坐标为(0,2)
∴满足条件的点共有3个,
故选B.
点评:此题主要考查了二次函数的性质,根据直径为4的⊙P与y轴相切,得出圆心的横坐标为2或-2是解题关键.
分析:首先求得函数的解析式,根据点P为抛物线上一动点,直径为4的⊙P与坐标轴相切,得出圆心的横坐标为2或-2,求出即可.
解答:(1)∵抛物线y=x2+bx+c经过(0,2)和点(2,2),
∴将点代入解析式

解得:

抛物线的表达式为:y=x2-2x+2,
∵点P为抛物线上一动点,
当直径为4的⊙P与y轴相切,
∴圆心的横坐标为2或-2,
当x=2,y=x2-2x+2=4-4+2=2,
∴点P的坐标为:(2,2),
当x=-2,y=x2-2x+2=4+4+2=10,
∴点P的坐标为:(-2,10),
当直径为4的⊙P与y轴相切,
∴圆心的纵坐标为2
y=x2-2x+2=2
解得:x=2或0,
∴点P的坐标为(0,2)
∴满足条件的点共有3个,
故选B.
点评:此题主要考查了二次函数的性质,根据直径为4的⊙P与y轴相切,得出圆心的横坐标为2或-2是解题关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
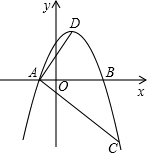 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=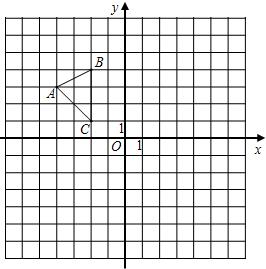 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.