题目内容
已知：直角三角形ABC中，∠C=90°，斜边AB=24cm，∠A=30°，则直角边BC=分析：根据直角三角形正余弦表达式及特殊角的三角函数分别计算出BC、AC的值，然后根据直角三角形面积公式得出斜边上的高．
解答：解：根据题意：
sin∠A=
=
，
∴BC=
AB=12cm，
cos∠A=
=
，
∴AC=
AB=12
，
设高为h，
根据直角三角形面积公式：
AC•BC=
AB•h，
h=
=6
，
故答案为12，6
．
sin∠A=
| BC |
| AB |
| 1 |
| 2 |
∴BC=
| 1 |
| 2 |
cos∠A=
| AC |
| AB |
| ||
| 2 |
∴AC=
| ||
| 2 |
| 3 |
设高为h，
根据直角三角形面积公式：
| 1 |
| 2 |
| 1 |
| 2 |
h=
| AC•BC |
| AB |
| 3 |
故答案为12，6
| 3 |
点评：本题主要考查了直角三角形正余弦表达式，特殊角的三角函数值及直角三角形面积公式，难度适中．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
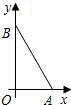已知一个直角三角形纸片OAB，其中∠AOB=90°，OA=2，OB=4．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB交于点C，与边AB交于点D．
