题目内容
已知等腰直角三角形ABC,斜边AB的长为2.以AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系,则点C的坐标是( )
分析:根据题意画出图形,由等腰三角形的性质即可求出点C的坐标.
解答: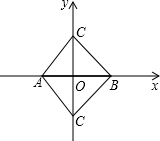 解:已知如图所示:
解:已知如图所示:
①当点C在y轴的正半轴时,
∵AB=2,AC=BC,∠ACB=90°,
∴OC=
AB=1,
∴点C的坐标是(0,1);
②当点C在y轴的负半轴时,由①可知:点C的坐标是(0,-1);
综上可知:点C的坐标是(0,1)或(0,-l),
故选C.
 解:已知如图所示:
解:已知如图所示:①当点C在y轴的正半轴时,
∵AB=2,AC=BC,∠ACB=90°,
∴OC=
| 1 |
| 2 |
∴点C的坐标是(0,1);
②当点C在y轴的负半轴时,由①可知:点C的坐标是(0,-1);
综上可知:点C的坐标是(0,1)或(0,-l),
故选C.
点评:本题考查了等腰直角三角形的性质以及坐标与图形性质,解题的关键是C的位置不确定,需要讨论.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知等腰直角三角形外接圆半径为5,则内切圆半径为( )
A、5
| ||
B、12
| ||
C、5
| ||
D、10
|
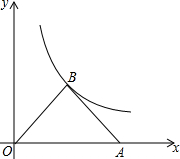 如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线
如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线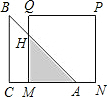 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合,求重叠部分的面积ycm2与时间ts之间的函数关系式.
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合,求重叠部分的面积ycm2与时间ts之间的函数关系式.